Cône de lumière
Cône de lumière
En physique, le cône de lumière est un objet fondamental de la relativité restreinte. C'est cet objet qui crée la distinction entre un évènement passé et un évènement futur.
Soit un évènement  singularisé, tous les autres évènements de l'espace-temps se divisent en trois catégories : le passé absolu et le futur absolu de
singularisé, tous les autres évènements de l'espace-temps se divisent en trois catégories : le passé absolu et le futur absolu de  d'une part — ces évènements se produisant à l'intérieur du cône, et l'ailleurs d'autre part — qui est constitué des autres évènements.
d'une part — ces évènements se produisant à l'intérieur du cône, et l'ailleurs d'autre part — qui est constitué des autres évènements.
Les événements intérieurs du cône peuvent être liés causalement avec  ; par contre les évènements situés dans l'ailleurs de
; par contre les évènements situés dans l'ailleurs de  sont dits causalement déconnectés de
sont dits causalement déconnectés de  et ne peuvent l'influencer ou être influencés par lui.
et ne peuvent l'influencer ou être influencés par lui.
Intervalle d'espace-temps
Un référentiel inertiel étant choisi, considérons deux événements séparés dans l'espace par la distance  et dans le temps par l'intervalle de temps
et dans le temps par l'intervalle de temps 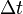 . En relativité restreinte, ces deux quantités ne sont pas invariantes par changement de référentiel.
. En relativité restreinte, ces deux quantités ne sont pas invariantes par changement de référentiel.
Par contre, en relativité restreinte, la quantité (notée formellement avec un carré)  est invariante par changement de référentiel, il en est de même pour son signe[1].
est invariante par changement de référentiel, il en est de même pour son signe[1].
En particulier, en fixant un événement noté  , on classe chaque événement de l'espace-temps en fonction du signe[2] de l'intervalle d'espace-temps qui le sépare de
, on classe chaque événement de l'espace-temps en fonction du signe[2] de l'intervalle d'espace-temps qui le sépare de  . Le signe de l'intervalle d'espace temps étant invariant par changement de référentiel, cette classification est indépendante de l'observateur et de son référentiel.
. Le signe de l'intervalle d'espace temps étant invariant par changement de référentiel, cette classification est indépendante de l'observateur et de son référentiel.
Le bord du cône
Les événements séparés par un intervalle  tel que
tel que 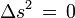 sont ceux qui sont à une distance spatiale
sont ceux qui sont à une distance spatiale  et une distance temporelle
et une distance temporelle 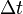 de
de  telles que
telles que  . C'est-à-dire que ces événements ne peuvent être joints depuis
. C'est-à-dire que ces événements ne peuvent être joints depuis  que par un message ou influence allant à la vitesse de la lumière. De plus, l'égalité
que par un message ou influence allant à la vitesse de la lumière. De plus, l'égalité  est l'équation du bord à trois dimensions d'un cône de révolution dans un espace à quatre dimensions.
est l'équation du bord à trois dimensions d'un cône de révolution dans un espace à quatre dimensions.
D'où le nom de cône de lumière.
L'intérieur du cône
Les événements séparés par un intervalle  tel que
tel que 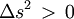 sont ceux qui sont à une distance spatiale
sont ceux qui sont à une distance spatiale  et une distance temporelle
et une distance temporelle 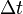 de
de  telles que
telles que 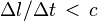 . C'est-à-dire que ces événements peuvent être joints depuis
. C'est-à-dire que ces événements peuvent être joints depuis  par un message ou influence allant à la vitesse strictement inférieure à celle de la lumière : c'est a priori réaliste. Ainsi, il peut y avoir une relation de causalité entre
par un message ou influence allant à la vitesse strictement inférieure à celle de la lumière : c'est a priori réaliste. Ainsi, il peut y avoir une relation de causalité entre  et l'un quelconque de ces événements.
et l'un quelconque de ces événements.
De plus, l'égalité 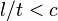 est l'équation de l'intérieur à quatre dimensions d'un cône dans un espace à quatre dimensions.
est l'équation de l'intérieur à quatre dimensions d'un cône dans un espace à quatre dimensions.
La partie supérieure de l'intérieur du cône contient tous les événements futurs que l'on peut joindre à partir de  .
.
La partie inférieure de l'intérieur du cône contient tous les événements passés à partir desquels on pouvait joindre  .
.
L'extérieur du cône
Les événements séparés par un intervalle  tel que
tel que  sont ceux qui sont à une distance spatiale
sont ceux qui sont à une distance spatiale  et une distance temporelle
et une distance temporelle 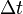 de
de  telles que
telles que  . C'est-à-dire que ces événements ne peuvent être joints depuis
. C'est-à-dire que ces événements ne peuvent être joints depuis  , car la vitesse de tout message ou influence est strictement inférieure à celle de la lumière en relativité restreinte : la jonction n'est pas réaliste. De plus, l'égalité
, car la vitesse de tout message ou influence est strictement inférieure à celle de la lumière en relativité restreinte : la jonction n'est pas réaliste. De plus, l'égalité  est l'équation de l'extérieur à quatre dimensions d'un cône dans un espace à quatre dimensions.
est l'équation de l'extérieur à quatre dimensions d'un cône dans un espace à quatre dimensions.
Les événements qui sont dans cet extérieur du cône sont dits ailleurs par rapport à  et ne peuvent être en relation causale directe avec lui.
et ne peuvent être en relation causale directe avec lui.
Voir aussi
Notes
- On a choisi ici la signature
 , en choisissant la signature (-,+,+,+) l'invariant serait
, en choisissant la signature (-,+,+,+) l'invariant serait 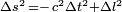
- En choisissant une autre signature, les signes de la classification sont inversés.
