En poursuivant votre navigation sur ce site, vous acceptez l'utilisation de cookies pour vous proposer des services et offres adaptés à vos centres d'intéréts.

Théorie du Chaos - partie 2

 

(suite de la partie 1) Théorie du Chaos

 

Transition d'une dynamique régulière vers le chaos [modifier]

Soit un système dynamique dépendant d'un paramètre μ :

frac{dx(t)}{dt} = f_{mu}(x(t),t)

Il arrive que la dynamique change de comportement lorsque le paramètre μ varie. On a pu mettre en évidence trois grands scénarios de passage d'une dynamique régulière à une dynamique chaotique lors de la variation d'un paramètre.

Scénario de Feigenbaum [modifier]

Feigenbaum a proposé un scénario dit : « par doublement de période » pour décrire la transition d'une dynamique régulière vers le chaos. Ce scénario trouve son origine dans le comportement de la suite logistique, qui est définie par récurrence par une application du segment [0, 1] dans lui-même :

x_{n+1} = mu , x_n (1 - x_n)

où n = 0, 1, … dénote le temps discret, x l'unique variable dynamique, et 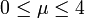0 le mu le 4 un paramètre[19]. La dynamique de cette application présente un comportement très différent selon la valeur du paramètre μ :

  • Pour 0 le mu < 3 , le système possède un point fixe attractif, qui devient instable lorsque μ = 3.
  • Pour 3 le mu < 3.57..., l'application possède un attracteur qui est une orbite périodique, de période 2n où n est un entier qui tend vers l'infini lorsque μ tend vers 3.57…
  • Lorsque μ = 3.57..., l'application possède un attracteur de Feigenbaum fractal (mais non étrange) découvert par le biologiste May (1976)[20].
  • Le cas μ = 4 avait été étudié dès 1947 par Ulam et von Neumann[21]. À noter qu'on peut dans ce cas précis établir l'expression exacte de la mesure invariante ergodique [22].
Bifurcation vers le chaos par doublement de période
Bifurcation vers le chaos par doublement de période

Lorsque le paramètre μ augmente, on obtient donc une succession de bifurcations de la régularité vers le chaos, résumée sur la figure ci-contre.


Scénario de Ruelle-Takens [modifier]

Par quasi-périodicité…

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Scénario de Pomeau-Manneville [modifier]

Par intermittence…

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Quelques exemples [modifier]

Articles liés [modifier]

Bibliographie [modifier]

Bibliothèque virtuelle [modifier]

  • David Ruelle ; Chaos, imprédictibilité et hasard, conférence de vulgarisation donnée en 2000 par l'auteur à l'Université de tous les savoirs, puis publiée dans : Qu'est-ce que l'Univers ? (éd. Y. Michaud), Odile Jacob (2000), 647-656. Texte complet disponible au format pdf.
  • Académie des sciences morales et politiques ; Le chaos, dans : Implications philosophiques de la science contemporaine (2001), groupe de travail présidé par Bernard d'Espagnat :
    • François Lurcat ; Le chaos & l'occident, format pdf.
    • Éric Bois ; De quelques enjeux philosophiques du phénomène du chaos, format pdf.
    • Débat, format pdf.
  • Predrag Cvitanovic´, Roberto Artuso, Ronnie Mainieri & Gábor Vattay ; The Chaos Webbook, (Version 11 - Décembre 2004). Ouvrage de référence en ligne écrit par Predrag Cvitanovic´ (Niels Bohr Institute, Copenhague) et ses collaborateurs.

Ouvrages de vulgarisation [modifier]

  • Amy Dahan Dalmedico, Jean-Luc Chabert & Karine Chemla (sous la direction de) ; Chaos & déterminisme, Points Sciences, Le Seuil (1992), ISBN 2-02-015182-0. Un ouvrage collectif au format poche, divisé en trois parties : Approches mathématiques, Physique & Calcul, et Quelques retours sur l'histoire et la philosophie, écrits par quelques-uns des meilleurs spécialistes actuels du domaine.
  • David Ruelle ; Hasard & Chaos, Collection Opus 89, Editions Odile Jacob (1991), ISBN 2-7381-0665-X. Un remarquable ouvrage d'introduction au chaos au format poche par un expert, professeur de physique théorique à l'Institut de hautes études scientifiques de Bures-sur-Yvette, et auteur de nombreuses contributions au domaine.
  • Pierre Bergé, Yves Pomeau & Monique Dubois-Gance ; Des rythmes au chaos, Collection Opus 64, Editions Odile Jacob (1997), ISBN 2-7381-0524-6. Un autre ouvrage d'introduction au format poche, par des spécialistes français.
  • Florin Diacu & Philip Holmes ; Celestial Encounters - The Origin of Chaos, Princeton University Press (1996), ISBN 0-691-00545-1. L'origine du "chaos" moderne se trouve dans les travaux pionniers d'Henri Poincaré réalisés à la fin du XIXe siècle à propos d'un vieux problème de mécanique newtonienne : le problème à N corps. Les auteurs du présent ouvrage, mathématiciens spécialistes du domaine, retracent élégamment l'histoire de ce problème et de ses développements de Poincaré à nos jours. Vulgarisation accessible à partir du premier cycle universitaire.
  • James Gleick, La Théorie du chaos, Albin Michel (1989), ISBN 2-226-03635-0. Réédité par Flammarion (1991), ISBN . Ouvrage écrit par un journaliste.

Textes techniques [modifier]

  • Pierre Bergé, Yves Pomeau & Christian Vidal ; L'ordre dans le chaos - Vers une approche déterministe de la turbulence, Hermann (1988), ISBN 2-7056-5980-3. Un ouvrage d'introduction au chaos par des experts français, accessible dès le premier cycle universitaire. Prix Henri Poincaré 1990 de l'Académie des Sciences.
  • T. W. B. Kibble & F.H. Berkshire ; Classical Mechanics, Prentice Hall (4e édition-1997), ISBN 058225972X. Un excellent cours d'introduction à la mécanique, des fondements newtoniens jusqu’aux formalismes plus avancés de Lagrange et de Hamilton. Kibble est professeur émérite de Physique Théorique de l'Imperial College de Londres. Pour cette 4e édition (avec un co-auteur), deux chapitres d'introduction aux idées de la théorie du chaos ont été inclus. Niveau : à partir du premier cycle universitaire. (N.B. : Il a existé une traduction française de l'édition précédente, publiée en son temps par Dunod.)
  • K. Alligood, T. Sauer & J. A. Yorke ; Chaos: An Introduction to Dynamical Systems, Springer-Verlag (1997), ISBN 0-387-94677-2.
  • David Ruelle ; Deterministic chaos: the science and the fiction, Proceedings of the Royal Society London A 427 (1990), 241-248.
  • Henri Poincaré ; Les méthodes nouvelles de la mécanique céleste, 3 volumes, Éditions Gauthiers-Villars (1892).
  • Jacques Hadamard ; Les surfaces à courbures opposées et leurs lignes géodésiques, Journal de Mathématiques Pures & Appliquées 4 (1898) 27. Pour une revue plus récente, voir e.g. la référence suivante : Pierre Pansu ; Le flot géodésique des variétés Riemanniennes à courbure négative, Séminaire Bourbaki 738 (1991) publié dans : Astérisque 201-203 (1991) 269-298.
  • Vladimir I. Arnold ; Mathematical Methods of Classical Mechanics, Springer-Verlag (2e édition-1989), ISBN 0-387-96890-3. Une synthèse de l'état de l'art en mécanique analytique (formalismes lagrangien & hamiltonien) avec l'accent mis sur l'interprétation géométrique de ces formalismes, par l'un des plus brillants mathématiciens du domaine. À partir du second cycle universitaire.
  • Vladimir I. Arnold, V.V. Kozlov & A.I. Neishtadt ; Mathematical Aspects of Classical and Celestial Mechanics, Encyclopaedia of Mathematical Sciences, Springer-Verlag (2e édition-1993). Une synthèse de l'état de l'art en mécanique céleste, par l'un des plus brillants mathématiciens du domaine (Arnold) et ses collaborateurs. À partir du second cycle universitaire.
  • Vladimir Arnold & André Avez ; Ergodic problems of classical mechanics, Advanced Book Classics, Addison-Wesley (1988), ISBN . Réédition d'un ouvrage classique écrit en 1968.
  • David Ruelle & Jean-Pierre Eckmann ; Ergodic theory of chaos and strange attractors, Review of Modern Physisc 57 (1985), 617-656.
  • Vladimir Damgov, Nonlinear and parametric phenomena - Applications in radiophysical and mechanical systems, World Scientific, Series on Nonlinear Sciences, 2004.

Aspects historiques [modifier]

  • Amy Dahan & David Aubin ; Writing the History of Dynamical Systems and Chaos : Longue Durée and Revolution, Disciplines and Culture, Historia Mathematica 29 (2002), 273-339. Texte complet disponible au format pdf.
  • Amy Dahan ; Le chaos a-t-il engendré une révolution scientifique ?, La Recherche (janvier 2000).
  • Amy Dahan ; Le difficile héritage de Henri Poincaré en systèmes dynamiques, in Greffe, J., Heinzmann, G., & Lorenz, K., (eds.) ; Henri Poincaré, science et philosophie, Berlin, Akademie Verlag & Paris, Blanchard (1997), 13-33.
  • David Aubin ; A Cultural History of Catastrophes and Chaos: Around the Institut des Hautes Études Scientifiques, France 1958-1980, Thèse de doctorat (Ph. D.), Princeton University (1998), UMI #9817022. Texte complet disponible au format pdf.

Notes [modifier]

  1. ↑ Pour un système dynamique différentiable décrit par une équation différentielle, deux degrés de liberté suffisent. Pour un système dynamique non différentiable décrit par une application discrète, un seul degré de liberté est suffisant.
  2. ↑ Bien sûr, un système complexe peut aussi posséder une dynamique d'une grande complexité : mentionnons par exemple les phénomènes météorologiques ou l'économie.
  3. ↑ Tien-Yien Li & James A. Yorke ; Period three implies chaos, American Mathematical Monthly 82 (1975), 985-992.
  4. ↑ Le lecteur notera que, outre le développement de l'informatique dans les années 1960-1970, l'acceptation de cette description probabiliste par la communauté des physiciens a certainement été facilitée par les grands succès obtenus depuis le début du XXe siècle en physique quantique, autre théorie de nature foncièrement probabiliste.
  5. ↑ James Gleick ; La Théorie du Chaos, chapitre L'expérimentateur, page 257 dans la version française. L'auteur a déclaré avoir paraphrasé le philosophe qui n'a jamais prononcé ces mots, contrairement à ce que la tournure de la phrase laisse entendre
  6. ↑ Rappelons qu'une équation différentielle d'ordre n peut toujours se ramener à un système de n équations différentielles couplées d'ordre un.
  7. ↑ Pierre-Simon Laplace ; Essai philosophique sur les probabilités, (Paris, 1814) ; Edition des « Maîtres de la pensée scientifique », Gauthier-Villars (Paris, 1921) pp. 3-4.
  8. ↑ Henri Poincaré ; Calcul des probabilités, Gauthier-Villars (Paris - 2e édition, 1912). Réimpression : Editions Jacques Gabay (Paris-1987).
  9. ↑ On a l'implication : scriptstyle{B Longrightarrow K}, la réciproque étant fausse en général. Les systèmes K et B possèdent une entropie de Kolmogorov-Sinaï positive.
  10. ↑ L'inverse du temps scriptstyle{tau} est appelé un exposant de Lyapounov.
  11. ↑ Le jury est composé de Weierstrass, Mittag-Lefflet et Hermite.
  12. ↑ June Barrow-Green ; Poincaré & the three-body problem, History of Mathematics (Vol. 11), American Mathematical Society & London Mathematical Society (1997).
  13. ↑ Lire e.g. : Jacques Laskar ; La stabilité du système solaire, dans : Amy Dahan Dalmedico, Jean-Luc Chabert & Karine Chemla (sous la direction de) ; Chaos & déterminisme, Points Sciences, Le Seuil (1992), ISBN 2-02-015182-0 ; et : Jacques Laskar ; Chaos in the Solar System, conférence pleinière donnée à TH2002 (Paris-Juillet 2002). Format pdf.
  14. ↑ G.J. Sussman & J. Wisdom ; Chaotic evolution of the solar system, Science 257 (1992), 56-62.
  15. ↑ La divergence n'est en général exponentielle que localement. Rappelons en effet qu'un système chaotique possède le plus souvent un espace des phases [[Compacité (mathématiques) |compact]], propriété qui permet l'existence d'un phénomène de récurrence.
  16. ↑ Edward N. Lorenz, Deterministic non-periodic flow, Journal of the Atmospheric Sciences 20(2) (1963), 130–141. Format pdf.
  17. ↑ Le titre n'est en fait pas de Lorenz, mais d'un autre météorologue, Philip Merilees, organisateur de la conférence ; Lorenz l'a découvert trop tard pour pouvoir en changer. Cf. Nicolas Witkowski : La chasse à l'effet papillon, Alliage 22 (1995), 46-53.
  18. ↑ Edward N. Lorenz ; Un battement d'aile de papillon au Brésil peut-il déclencher une tornade au Texas ?, Alliage 22 (1993), 42-45. Traduction française du texte de la conférence de 1972, publié (en anglais) dans : The essence of chaos, The Jessie and John Danz Lecture Series, University of Washington Press (1993). Ce livre contient une série de conférences de vulgarisation données à l'université de Washington (Seattle) en 1990.
  19. ↑ Lorsque le paramètre scriptstyle{mu} devient supérieur à quatre, l'application sort de l'intervalle [0, 1].
  20. ↑ R.M. May ; Nature 261 (1976), 459.
  21. ↑ Stanislas Ulam & John Von Neumann ; Bulletin of the American Mathematical Society 53 (1947), 1120.
  22. ↑ Pierre Collet & Jean-Pierre Eckmann ; Iterated Maps on the Interval as Dynamical Systems, Birkhaüser (1980).

Liens externes [modifier]

Portail des mathématiques
Portail de la physique

Récupérée de « http://fr.wikipedia.org/wiki/Th%C3%A9orie_du_chaos »


17/11/2007
0 Poster un commentaire

A découvrir aussi


⨯

Inscrivez-vous au blog

Soyez prévenu par email des prochaines mises à jour

Rejoignez les 525 autres membres