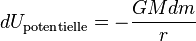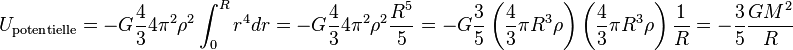Loi universelle de la gravitation
Loi universelle de la gravitation
La loi de la gravitation ou loi de l'attraction universelle, découverte par Isaac Newton, est la loi décrivant la gravitation comme une force responsable de la chute des corps et du mouvement des corps célestes, et de façon générale, de l'attraction entre des corps ayant une masse, par exemple les planètes, les satellites naturels ou artificiels. Cet article présente essentiellement les aspects de la mécanique classique de la gravitation, et non pas la relativité générale qui procède d'un cadre plus général dans un nouveau paradigme.
Sommaire
[masquer]Expression mathématique selon Isaac Newton
Deux corps ponctuels de masses respectives 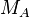 et
et  s'attirent avec des forces de mêmes valeurs (mais vectoriellement opposées), proportionnelles à chacune des masses, et inversement proportionnelle au carré de la distance qui les sépare. Cette force a pour direction la droite passant par le centre de gravité de ces deux corps.
s'attirent avec des forces de mêmes valeurs (mais vectoriellement opposées), proportionnelles à chacune des masses, et inversement proportionnelle au carré de la distance qui les sépare. Cette force a pour direction la droite passant par le centre de gravité de ces deux corps.
La force exercée sur le corps  par le corps
par le corps  est vectoriellement donnée par
est vectoriellement donnée par
 et
et  en kilogramme (kg); d en mètre (m);
en kilogramme (kg); d en mètre (m);  et
et  en newton (N)
en newton (N)
où G est la constante gravitationnelle, elle vaut dans les unités SI, le CODATA 2010 [1]
Énergie potentielle de gravitation
Voici le calcul menant à l'expression de l'énergie potentielle de gravitation d'un corps de masse m à une distance R d'un corps de masse M produisant le champ de gravitation :
D'où :
Cette formule est très apparentée à celle de l'électrostatique, qui est issue de la loi de Coulomb (qui est simplement la loi de gravitation universelle traduite en électricité). Ainsi, tous les calculs de gravimétrie sont transposables en électrostatique et réciproquement, ce qui est une économie de pensée considérable.
Énergie potentielle d'une sphère homogène
Soit un corps sphérique de rayon R et de masse volumique uniforme  .
.
On peut démontrer que son énergie potentielle interne  est égale à :
est égale à :
Histoire de la découverte de la force de gravitation
Travaux antérieurs à Newton
Chargé par Tycho Brahe d'étudier le mouvement des planètes, Johannes Kepler écrit ses conclusions dans l'ouvrage « Astronomia nova » où sont indiquées trois lois que vérifie le mouvement des planètes et des astres, ces lois seront par la suite appelées « lois de Kepler ». Dans « Harmonices Mundi », Kepler écrivit : « C'est comme si une force émane du Soleil ». Il y étudia la piste d'une force magnétique.
Sur ces bases, à partir de la 3e loi de Kepler, Isaac Newton développa sa théorie sur la gravitation.
Compatibilité de l'hypothèse newtonienne avec la troisième loi de Kepler
On part de la 3e loi de Kepler :
Avec a, demi grand-axe, T période (année de l'astre), k constante de gravitation.
Cela se lit ainsi : pour chaque astre du système solaire, la pulsation 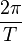 moyenne d'un astre au carré multiplié par la distance moyenne à l'astre central (le Soleil dans le cas des planètes), le demi grand-axe, à la puissance 3, est identique et égale à k.
moyenne d'un astre au carré multiplié par la distance moyenne à l'astre central (le Soleil dans le cas des planètes), le demi grand-axe, à la puissance 3, est identique et égale à k.
Dans le cas d'une orbite circulaire, la 3e loi de Kepler s'écrit :
Soit r, rayon de l'orbite circulaire,
Ou bien, en divisant les deux termes de l'équation par 
Selon la loi fondamentale de la dynamique (seule la force de gravitation  est prise en compte):
est prise en compte):
On connait l'accélération centrifuge, c'est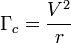 , la circonférence de l'orbite circulaire est
, la circonférence de l'orbite circulaire est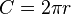 , la vitesse tangentielle est donc
, la vitesse tangentielle est donc . L'accélération centrifuge s'ensuit :
. L'accélération centrifuge s'ensuit :
Puisque, en cas d'un orbite circulaire, la seule accélération est centripète, donc de même intensité que l'accélération centrifuge, en travaillant en module, selon la loi fondamentale de la dynamique, et la 3e loi de Kepler on a :
En posant  , avec G, constante de gravitation universelle et
, avec G, constante de gravitation universelle et  , masse du soleil, on obtient :
, masse du soleil, on obtient :
 , loi de la gravitation reformulée par Newton.
, loi de la gravitation reformulée par Newton.
Cela démontre que l'hypothèse d'une force agissant à distance entre objets massifs telle qu'émise par Newton est compatible avec la 3e loi de Kepler, au moins pour des orbites circulaires.
Retentissement de la découverte
|
|
Cet article ne cite pas suffisamment ses sources (juillet 2008).
Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ». (Modifier l'article) |
Isaac Newton en 1684 utilise pour la première fois cette loi dans le De motu corporum in gyrum (sur le mouvement), mais pour des astres supposés ponctuels. Il est vraisemblable qu'au cours de la rédaction de cet opuscule, en 1685, il réalise que sa loi universelle est plus profonde car elle est « plus simple »[réf. nécessaire]. Il découvre que tout en astronomie s'en déduit, et qu'il peut même appliquer sa loi à la pesanteur, unifiant ainsi les deux nouveaux mondes de Galilée[réf. nécessaire] : la mécanique terrestre et la mécanique céleste. Il demandera à Halley un délai pour mettre « tout ce fatras »[réf. nécessaire] au propre : ce qui exigera de sa part un effort colossal. En 1687, paraîtront les Principia, qui est un monument de la pensée humaine : des dizaines de théorèmes y sont démontrés, montrant la voie pour la recherche du XVIIIe siècle. Pour la première fois, est mise pleinement en acte la pensée de Galilée : le grand livre de la Nature peut s'expliquer par les mathématiques. Ainsi peut-on considérer Newton comme le « fondateur de la physique mathématique »[réf. nécessaire]. Tous ses rivaux (Hooke, Huygens, etc.) sont relégués à l'avant Newton, un peu comme après 1905, on parlera de avant/après Einstein. Mais cela n'est évidemment point vrai ; et Newton reprendra à son compte l'aphorisme de Nicole Oresme :
« Si j'ai pu voir un peu au-delà, c'est que j'étais porté par des épaules de géants ». Il est clair que la loi en 1/r² est déjà connue de Hooke, Halley[réf. nécessaire]; mais personne ne l'a énoncée ainsi. Newton a surtout été acclamé pour sa reformulation des lois de Kepler, alors que c'est un théorème parmi bien d'autres.
Les Principia sont très difficiles à lire : il fallait pour suivre le cheminement de la pensée de Newton comprendre « l'ultime raison »[réf. nécessaire], le 0/0 du calcul infinitésimal. Newton s'en attribue l'invention, mais une polémique l'oppose à Leibniz sur ce sujet. Leibniz en semble plutôt l'inventeur.
D'autre part, Newton franchit un Rubicon qui provoquera les tollés de l'élite scientifique de l'époque : hypotheses non fingo, je ne feins pas d'hypothèse. Explicitement : je rétablis en physique cette chose « interdite » depuis Aristote[citation nécessaire] : l'action « instantanée à distance ». Les cartésiens refuseront cela, de même que, en Allemagne, Leibniz, qui imagine un principe de rotation harmonique de l'éther (c'est-à-dire que l'éther tourne en même temps que les planètes, selon les lois de Kepler, ce qui les charrient).
En conséquence, le temps de réception des travaux de Newton en France et en Allemagne sera très long (presque 30 ans). Newton lui-même a essayé de trouver la cause de cette attraction, en vain.
Validité de la loi de Newton dans le cadre de la théorie de la relativité
Vers 1900, on sait qu'il reste à expliquer un résidu dans la précession de la trajectoire de la planète Mercure autour du Soleil. Bien qu'il n'ait pas cherché à résoudre cette anomalie, Einstein expliquera ces fameuses 43 secondes d'arc par siècle, en inventant sa théorie de la gravitation appelée relativité générale en 1915.
La loi de Newton n'est qu'une approximation de la gravitation relativiste, valable lorsque (v/c)2 << 1 (où v désigne la vitesse relative des corps et c la vitesse de la lumière). Le philosophe des sciences Thomas Samuel Kuhn n'hésite pas à affirmer que la théorie d'Einstein ne peut être acceptée que si l'on tient celle de Newton pour fausse. Selon lui, l'affirmation que la loi de Newton fournit une bonne solution approchée lorsque les vitesses relatives des corps considérés sont petites en comparaison de la vitesse de la lumière est une objection des successeurs des positivistes logiques. Toujours selon lui, la théorie d'Einstein représente un changement majeur de paradigme par rapport à la théorie newtonienne, au même titre que l'astronomie de Copernic a été un changement de paradigme par rapport à l'astronomie de Ptolémée[2] .
La loi de Newton est incapable de s'appliquer aux trous noirs, ni à la déviation de la lumière par la gravitation, ou autres phénomènes observés au XXe siècle.
On notera qu'il existe trois autres forces fondamentales en physique :
- la force électromagnétique (courants électriques, aimants, etc.),
- l'interaction faible,
- l'interaction forte (cohésion des noyaux),
ces trois dernières forces fondamentales pouvant être unifiées.
Aspects philosophiques
Un philosophe, Claude Henri de Rouvroy, comte de Saint-Simon, a bâti une théorie philosophique dans les années 1820, selon laquelle Dieu est remplacé par la gravitation universelle.
David Hume voyait dans les Principia le modèle de la science, qu'il voulait appliquer à la philosophie[3].
Notes et références
- CODATA de 2010.[1] [archive], CADATA 2010
- Thomas Kuhn, La Structure des révolutions scientifiques, Flammarion, pp. 141-142 (première édition en 1962)
- Enquête sur l'Entendement Humain, I
Aidez à améliorer cette page
Qu’est-ce que ceci ?
×Wikipédia aimerait avoir votre avis sur cette page. Partagez votre retour quant à cette page avec les contributeurs, et aidez à améliorer Wikipédia.



![\Delta U_{\text{potentielle}}=\int_\infty^R \vec{F}\cdot\vec{dl} = \int_\infty^R\frac{-GMm}{r^2} dr\cdot\vec{u_r}\cdot\vec{u_r}\ = GMm\int_\infty^R\frac{-dr}{r^2} = GMm \left[\frac{1}{r}\right]_\infty^R](https://upload.wikimedia.org/math/1/2/d/12d9cb3d8fcd8c03e71a6e91fa1a1692.png)