Horizon cosmologique
Horizon cosmologique
Un article de Wikipédia, l'encyclopédie libre.
L'horizon cosmologique ou horizon cosmique est un terme d'astronomie qui désigne la limite de l'univers observable depuis un point donné (en général la Terre). Selon le contexte, il correspond soit à la limite d'où un rayonnement électromagnétique peut être issu, ou alors la limite d'où un signal de quelque nature que ce soit (neutrinos ou ondes gravitationnelles) peut être reçu. En pratique, les moyens observationnels actuels sont pour l'heure (2007) incapables de détecter des neutrinos ou ondes gravitationnelles primordiales. Plus généralement, un modèle cosmologique donné peut ou non contenir un tel horizon, c'est-à-dire des régions inaccessibles à l'observation d'un observateur donné.
L'horizon cosmologique est défini par analogie à l'horizon terrestre. De même que la courbure de la terre limite la vision de celle-ci depuis un point fixe sur sa surface, la taille de l'univers et la vitesse de déplacement de la lumière font qu'il est impossible de voir certains objets célestes (galaxies et amas de galaxies dans ce cas) trop éloignés.
L'âge de l'univers est d'environ 13,7 milliards d'années. Par conséquent il ne nous est possible de voir que les objets dont la lumière aura voyagé pendant moins de 13,7 milliards d'années. L'univers est ainsi partagé entre une partie visible (la plus proche) et une partie invisible (la plus éloignée), la limite entre les deux zones constituant l'horizon cosmologique. Au contraire de celles de la partie visible, les galaxies situées dans la partie invisible sont trop lointaines pour que leur lumière ait eu le temps de parvenir jusqu'à nous.
Cette définition de l'horizon cosmologique ne dépend pas de l'état d'expansion de l'univers. Mais certes la position actuelle de cet horizon en dépend. Si l'univers n'était pas en expansion, la limite de visibilité d'un photon atteignant la Terre se situerait à 13,7 milliards d'années-lumière. Cependant, du fait de l'expansion de l'univers, l'objet de l'horizon cosmologique qui a émis ce photon s'est déplacé pendant la durée de voyage de la lumière et est donc situé aujourd'hui à plus de 13,7 milliards d'années-lumière. Remarquons toutefois que le photon reçu aura voyagé pendant 13,7 milliards d'années, ce qui constitue finalement une mesure utile de la distance de l'horizon cosmologique (c'est en quelque sorte une « distance temporelle »).
En pratique, les signaux les plus lointains qui nous parviennent viennent du fond diffus cosmologique. Ce rayonnement emplit tout l'univers, mais la région d'où est issu le rayonnement que nous détectons est appelé, pour des raisons évidentes, surface de dernière diffusion. Les modèles cosmologiques utilisés de nos jours, basés sur le modèle standard de la cosmologie et les équations de Friedmann, indiquent que la surface de dernière diffusion se trouverait actuellement (voir ci-dessous) à environ 46 milliards d'années-lumière de l'observateur.
C'est ce chiffre qui caractérise habituellement la distance de l'horizon cosmologique.
Sommaire[masquer] |
Calcul de la taille de l'horizon cosmologique [modifier]
Il est délicat de définir des distance en cosmologie car ces distances varient au cours du temps par suite de l'expansion de l'univers (elles augmentent donc). Le concept de distance dépend beaucoup du moyen de mesure utilisé. Ainsi, les notions de distance angulaire (basée sur la taille angulaire d'un objet de taille connue) ou de distance de luminosité (basée sur le flux lumineux reçu d'un objet de luminosité connue) sont-elles différentes. Quand on parle de la taille de l'horizon, on entend distance séparant un observateur donné de l'objet le plus lointain qu'il puisse observer et rapporté à sa position actuelle, c'est-à-dire à l'époque où son temps cosmique est le même que celui de l'observateur. Les concepts de distance de luminosité ou de distance angulaires sont inadaptés pour les objets les plus distants car les objets situés à l'horizon ne sont pas détectables dans la pratique (la vision étant bornée à la surface de dernière diffusion).
La distance de l'horizon se calcule suivant une formule du type
 ,
,
où c correspond à la vitesse de la lumière, t * et t0 correspondent respectivement à l'époque d'émission du signal le plus distant détectable et l'époque actuelle, et où la fonction z(t) donne le décalage vers le rouge d'un signal reçu aujourd'hui après avoir été émis au temps t. Une façon intuitive d'interpréter ce résultat est de dire qu'un photon parcours la distance  entre les instants t et t + dt, mais que cette distance s'est aujourd'hui allongée d'un facteur 1 + z(t) du fait de l'expansion de l'univers. Pour des époques récentes, 1 + z(t) est proche de 1 car les distances n'ont pas beaucoup bougé depuis lors, mais 1 + z(t) est significativement plus grand pour les époques plus anciennes.
entre les instants t et t + dt, mais que cette distance s'est aujourd'hui allongée d'un facteur 1 + z(t) du fait de l'expansion de l'univers. Pour des époques récentes, 1 + z(t) est proche de 1 car les distances n'ont pas beaucoup bougé depuis lors, mais 1 + z(t) est significativement plus grand pour les époques plus anciennes.
Pour calculer cette quantité, il faut connaître la relation z(t), c'est-à-dire la relation entre le décalage vers le rouge de la lumière émise par d'un objet et l'âge de l'univers à l'époque où celui-ci a émis le rayonnement reçu aujourd'hui. En d'autre terme, il faut connaître la relation entre le facteur d'échelle et le temps cosmique. Cette relation est établie par les équations de Friedmann dont c'est précisément l'objet. On trouve alors, sous certaines hypothèse, la relation suivante :
 ,
,
où H0 représente l'actuel taux d'expansion de l'univers (la constante de Hubble) et les différentes quantités Ω correspondent aux paramètres de densité des différentes espèces présentes dans l'univers, à savoir rayonnement et particules de masse nulle (r), matière non relativiste (matière baryonique et matière noire, m) et constante cosmologique (Λ) mesurés aujourd'hui.
Application au modèle standard de la cosmologie [modifier]
Le modèle standard de la cosmologie bâti à partir de l'ensemble des observations cosmologiques (et compatibles avec elles) indique que la densité d'énergie sous forme de rayonnement est négligeable devant les autres formes (matière et énergie noire), ce qui équivaut à dire que le terme 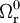 peut être négligé. De plus, le modèle exclut une valeur notable de la courbure spatiale, ce qui signifie que la somme des paramètre de densité vaut 1. Au final, il reste donc
peut être négligé. De plus, le modèle exclut une valeur notable de la courbure spatiale, ce qui signifie que la somme des paramètre de densité vaut 1. Au final, il reste donc
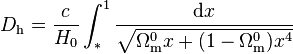 .
.
La quantité c / H0 est appelée rayon de Hubble. Avec la valeur communément admise de 70 kilomètres par seconde et par mégaparsec pour la constante de Hubble, la rayon de Hubble est d'environ 14 milliards d'années lumière[1]. Le terme dans l'intégrale ne peut être calculé analytiquement, mais une intégration numérique peut être effectuée sans difficulté en prenant pour Ωm la valeur communément admise d'environ 0,3. L'on trouve alors que l'intégrale est légèrement supérieurs à trois, que la borne d'intégration soit de 0 (on considère la distance maximale parcourue par tout signal émis depuis le Big Bang) ou d'un millième (corrspondant à un photon du fond diffus cosmologique, émis lors de la recombinaison. Au final, on retrouve bien la valeur de l'ordre de 45 milliards d'années lumière annoncée plus haut.
Cas particuliers [modifier]
Dans le cas où l'univers possède la densité critique et n'est composé que d'une espèce, dont le rapport de la pression à la densité d'énergie est w, on a
 .
.
Cette intégrale peut être évalué dans plus cas
Univers de radiation (w = 1/3) [modifier]
On a immédiatement
 ,
,
l'égalité ci-dessus étant approximativement car on n'a pas tenu compte de la valeur exacte de la borne inférieure (prise à 0 ici alors qu'elle pourrait être prise à une valeur légèrement positive). Dans ce cas, la taille de l'horizon correspond exactement au rayon de Hubble.
Univers de poussière (w = 0) [modifier]
On a désormais
 .
.
Dans ce cas, la taille de l'horizon correspond exactement au double du rayon de Hubble.
Univers à équation d'état constante [modifier]
Plus généralement, on a, dans le cas où w est constant et supérieur à − 1 / 3,
 .
.
D'une manière générale, plus l'équation d'état est « dure » (c'est-à-dire w grand), plus la taille de l'horizon est faible en unité du rayon de Hubble. Ceci peut être rendu plus explicite en utilisant la relation existant entre âge de l'univers t0et rayon de Hubble. Les équations de Friedmann indiquent que
 .
.
En combinant ces deux derniers résultats, il vient
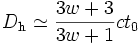 .
.
Ce résultat tend vers ct0 quand w tend vers l'infini. Cela s'interprète par le fait que cette limite correspond en fait au cas idéalisé où la matière tend à être incompressible (une variation de pression arbitrairement grande donnant lieu à une petite variarion de densité, ce qui est le cas si P = wρ est grand car alors  ). Dans ce cas, une telle matière a tendance à arrêter sa phase d'expansion le plus rapidement possible (elle s'oppose à une variation de son volume), ce qui fait que la phase d'expansion qui suit immédiatement le Big Bang s'arrête très vite, et que l'expansion tend à cesser. Dans un tel cas, on est dans une situation identique à celle de l'espace de Minkowski où au bout du temps t0 on peut recevoir des signaux distants de ct0. À noter cependant que le cas w > 1 est a priori physiquement irréaliste, car l'équation d'état est acausale : la vitesse du son dans un tel fluide, donnée par
). Dans ce cas, une telle matière a tendance à arrêter sa phase d'expansion le plus rapidement possible (elle s'oppose à une variation de son volume), ce qui fait que la phase d'expansion qui suit immédiatement le Big Bang s'arrête très vite, et que l'expansion tend à cesser. Dans un tel cas, on est dans une situation identique à celle de l'espace de Minkowski où au bout du temps t0 on peut recevoir des signaux distants de ct0. À noter cependant que le cas w > 1 est a priori physiquement irréaliste, car l'équation d'état est acausale : la vitesse du son dans un tel fluide, donnée par  dépasse celle de la lumière. À noter aussi qu'à l'inverse l'intégrale divergence quand w tend vers la valeur -1/3 (voir ci-dessous).
dépasse celle de la lumière. À noter aussi qu'à l'inverse l'intégrale divergence quand w tend vers la valeur -1/3 (voir ci-dessous).
Univers de Milne (w = - 1/3) [modifier]
L'univers de Milne correspond à un espace vide de matière. Dans ce cas, tous les paramètres de densité sont nuls, ce qui formellement, du point de vu des équations de friedmann, peut s'interpréter comme un univers ayant la densité critique et un paramètre d'équation d'état w égal à -1/3. Il vient
 .
.
La primitive à calculer donne un logarithme. Il faut ici prendre soigneusement en compte la valeur de la borne inférieure. Si elle est nulle ( ), alors l'intégrale est infinie. Ce résultat tend à indiquer qu'il n'y a alors pas d'horizon, c'est-à-dire que toute région de l'univers est accessible à l'observation. Ceci peut se comprendre en remarquant que l'univers de Milne peut être vu comme une portion de l'espace de Minkowski, avec une origine d'où sont issues les particules fictives qui marquent l'expansion de l'univers en se déplaçant à vitesse constante (voir Univers de Milne). Dans un tel cas, toute les lignes d'univers de ces particules fictives d'intersectent les unes les autres à l'origine et sont donc toutes dans le cône de lumière passé des unes et des autres, ce qui fait que la totalité de l'univers est nécessairement observable. Si par contre on met une orne inférieure non nulle à l'intégrale, on impose de ne recevoir que des signaux dont le décalage vers le rouge n'excède pas une certaine valeur, c'est-à-dire issues de particules dont la vitesse n'excède pas une certaine valeur. Dans ce cas, seule une portion finie de cet univers est effectivement accessible.
), alors l'intégrale est infinie. Ce résultat tend à indiquer qu'il n'y a alors pas d'horizon, c'est-à-dire que toute région de l'univers est accessible à l'observation. Ceci peut se comprendre en remarquant que l'univers de Milne peut être vu comme une portion de l'espace de Minkowski, avec une origine d'où sont issues les particules fictives qui marquent l'expansion de l'univers en se déplaçant à vitesse constante (voir Univers de Milne). Dans un tel cas, toute les lignes d'univers de ces particules fictives d'intersectent les unes les autres à l'origine et sont donc toutes dans le cône de lumière passé des unes et des autres, ce qui fait que la totalité de l'univers est nécessairement observable. Si par contre on met une orne inférieure non nulle à l'intégrale, on impose de ne recevoir que des signaux dont le décalage vers le rouge n'excède pas une certaine valeur, c'est-à-dire issues de particules dont la vitesse n'excède pas une certaine valeur. Dans ce cas, seule une portion finie de cet univers est effectivement accessible.
Univers en accélération (w < -1/3) [modifier]
Dans le cas où le paramètre de l'équation d'état est inférieur à -1/3, l'intégrale diverge également pour une borne inférieure nulle
![D_\mathrm{h} = \frac{c}{H_0} \frac{2}{3 w + 1} \left[1 - \left(\frac{1}{1 + z_*}\right)^{\frac{3 w + 1}{2}} \right]](https://upload.wikimedia.org/math/4/4/1/44133eb2418664624a967ce6a5e90240.png) .
.
Il n'y a donc pas d'horizon cosmologique dans un tel espace, et en particulier pour l'univers de de Sitter.
Relation avec les théorèmes sur les singularités [modifier]
Ces résultats, en particulier le fait que l'univers possède un horizon quand le paramètre de l'équation d'état w est toujours supérieur à -1/3 s'avère être un cas particulier des théorèmes sur les singularités de Stephen Hawking et Roger Penrose. La contrainte imposée à w est en effet équivalent à la condition forte sur l'énergie, supposée pour permettre la validité de ces théorèmes. Une autre conséquence est que l'univers est alors, dans le cadre de la relativité générale, nécessairement issu d'une singularité gravitationnelle[2]. Il est cependant relativement avéré aujourd'hui que la condition forte sur l'énergie n'a pas forcément été respectée dans l'univers primordial (voir ci-dessous). Dans ce cadre, le fait que l'univers observable s'étende sur une région finie ne préjuge pas du fait qu'il soit issu d'une singularité.
Relation avec le problème de l'horizon [modifier]
En observant l'univers le plus loin possible dans deux directions opposées, on voit des régions séparées du double de la taille de l'horizon. Ces deux régions n'ont par définition pas eu la possibilité de communiquer entre elles. Il serait dans ce cas logique de s'attendre à ce que ces régions possèdent des propriétés différentes. Observationnellement il n'en est rien. Ce fait observationnel est appelé du nom de problème de l'horizon. La solution au problème de l'horizon s'obtient en considérant un scénario dans lequel la taille de l'univers observable (délimité par la limite de la surface de dernière diffusion, et en tenant compte de la borne inférieure d'intégration non nulle, 1 / (1 + z * ) ne correspondant pas du tout à la taille réelle de l'horizon, considérée en prenant une borne d'intégration nulle (ou arbitrairement petite, si l'on considère par exemple que les lois dela physique telles que nous les connaissons commencent à être valable au sortir de l'ère de Planck). Pour ce faire, l'on est amené à considéré un scénario où l'évolution du taux d'expansion de l'univers est significativement différentes à des époques anciennes (correspondant aux petites valeurs de x dans l'intégrale). Les scénarios sont amenés alors à considérer des situations où l'expression  , proportionnelle au rapport du taux d'expansion à l'époque où le facteur d'échelle était x fois plus petit qu'aujourd'hui au taux d'expansion actuel, doit être remplacé par une expression qui tend vers 0 (ou en tout cas est très petite) quand x tend vers 0. Cela peut se produire si la matière qui existe à cette époque possède un paramètre w inférieur à -1/3.
, proportionnelle au rapport du taux d'expansion à l'époque où le facteur d'échelle était x fois plus petit qu'aujourd'hui au taux d'expansion actuel, doit être remplacé par une expression qui tend vers 0 (ou en tout cas est très petite) quand x tend vers 0. Cela peut se produire si la matière qui existe à cette époque possède un paramètre w inférieur à -1/3.
Voir aussi [modifier]
- Horizon des événements
- Univers observable
- Fond diffus cosmologique
- Fond cosmologique de neutrinos
- Fond cosmologique d'ondes gravitationnelles
- Problème de l'horizon
- Horizon (trou noir)
- Univers de Milne
- Distance de l'horizon cosmologique dans un univers de Friedmann
Références [modifier]
Note [modifier]
- ↑ Cette valeur, divisée par la vitesse de la lumière est très proche de l'âge de l'univers. Si cette circonstance est fortuite dans le modèle standard, elle ne l'est pas dans d'autres modèles, comme celui de Friedmann.
- ↑ Voir (en) Stephen W. Hawking et G. F. R. Ellis, The large scale structure of space-time, Cambridge University Press, coll. « Cambridge Monographs on Mathematical Physics », 1975, 400 pages (ISBN 0521099064), chapitre 8, pages 256 à 298.
 ,
, 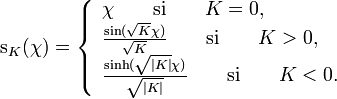
![\mathrm{d}s^2 = a^2(\eta) \left[\mathrm{d} \eta^2 - \mathrm{d} \chi^2 - \mathrm{s}_K^2(\chi) \left(\mathrm{d}\theta^2 + \sin^2\theta\mathrm{d}\varphi^2 \right)\right]](https://upload.wikimedia.org/math/1/c/6/1c61870b8e552ba878320c32724568f6.png) .
. 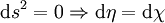 .
. 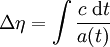 ,
,  .
.  ,
,  .
.  ,
,  ,
,  .
.  ,
,  , d'où
, d'où
 .
.  ,
,  ,
,  .
.  selon
selon ,
,  ,
,  ,
,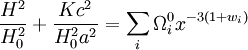 ,
,  étant les paramètres de densité actuels, définis par le rapport
étant les paramètres de densité actuels, définis par le rapport  . En évaluant cette équation aujourd'hui (où
. En évaluant cette équation aujourd'hui (où  ,
,  ,
,  .
.  .
.  .
.