Atome - Partie 2
Les modèles présentés dans cette section sont trop éloignés de la réalité pour pouvoir être utilisés. Ils ne sont présentés ici qu'à titre historique.
Le modèle de J.J. Thomson ou modèle du far aux pruneaux (plum-pudding) [modifier]
Avec la découverte de l'électron en 1897, on savait que la matière était composée de deux parties : une négative, les électrons, et une positive. Dans le modèle imaginé alors par Joseph John Thomson, les électrons, particules localisées, baignaient dans une « soupe » positive, à l'image des pruneaux dans le far breton (ou dans le plum-pudding pour les Britanniques ou encore comme des raisins dans un gateau). Ce modèle fut invalidé en 1911 par l'expérience d'un de ses anciens étudiants, Ernest Rutherford.
Vous pouvez aussi consulter la page en anglais
Le modèle planétaire de Rutherford [modifier]
L'expérience de Rutherford met en évidence que les charges positives ne sont pas « étalées » entre les électrons, mais sont concentrées en de petits points. Il bombarda une fine feuille d'or par un faisceau de particules alpha (particules de charges électriques positives). Il observa que les particules étaient déviées faiblement, ce qui ne correspondait pas au résultat prévu par le modèle de Thomson, pour lequel elles n'auraient pas dû la traverser.
Rutherford imagine donc un modèle planétaire : l'atome est constitué d'un noyau positif autour duquel tournent des électrons négatifs. Entre le noyau - très petit par rapport à l'atome (environ 100 000 fois) - et ses électrons, un très grand vide existe.
Ce modèle fut très vite mis en défaut par les équations de Maxwell d'une part, qui prédisent que toute charge accélérée rayonne de l'énergie, et par les expériences montrant la quantification des niveaux d'énergie d'autre part.
Modèles approchés couramment employés [modifier]
Le modèle des sphères dures [modifier]
Le modèle le plus simple pour représenter un atome est une boule indéformable. Ce modèle est très utilisé en cristallographie. Une molécule peut se voir comme plusieurs boules accolées, un cristal comme des boules empilées. On utilise parfois une représentation « éclatée » : les atomes sont représentés comme des petites boules espacées, reliées par des traits, permettant de faire ressortir les directions privilégiées, les angles et de visualiser le nombre des liaisons.
Ce modèle correspond bien à certaines propriétés de la matière, comme par exemple la difficulté de comprimer les liquides et les solides, ou bien le fait que les cristaux ont des faces bien lisses. En revanche, il ne permet pas d'expliquer d'autres propriétés, comme la forme des molécules : si les atomes n'ont pas de direction privilégiée, comment expliquer que les liaisons chimiques révèlent des angles bien définis ?
Le modèle de Bohr [modifier]
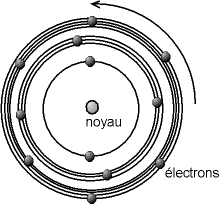
Un modèle fut développé par Niels Bohr en 1913 à partir des propriétés mises en évidence par Planck et Rutherford. Dans le modèle des sphères dures, l'atome est un objet entier, indécomposable. Or, on sait depuis le milieu du XIXe siècle que l'on peut en « arracher » des particules portant une charge électrique négative, les électrons. Dans le modèle de Bohr, l'atome est composé d'un noyau chargé positivement, et d'électrons tournant autour, les rayons des orbites des électrons ne pouvant prendre que des valeurs bien précises.
Le noyau est très compact, d'un diamètre d'environs 10-15 à 10-14 m, c'est-à-dire que le noyau est cent mille à un million de fois plus petit que l'atome ; il porte une charge électrique positive. C'est aussi la partie la plus lourde de l'atome, puisque le noyau représente au moins 99,95% de la masse de l'atome. Les électrons sont ponctuels, c'est-à-dire que leur rayon est admis quasi nul (tout du moins plus petit que ce que l'on peut estimer). Ils portent une charge négative. Pour des raisons de lisibilité, le schéma ci-dessous n'est donc pas à l'échelle, en ce qui concerne les dimensions du noyau et des électrons, ni aussi pour les rayons des différentes orbites (on notera ici que le nombre d'électrons sur les orbites n'est pas prédit par le modèle).
Cette vision permet de décrire les phénomènes spectroscopiques fondamentaux, c'est-à-dire le fait que les atomes absorbent ou émettent seulement certaines longueurs d'onde (ou couleur) de lumière ou de rayons X. En effet, les électrons ne pouvant tourner que sur des orbites définies, le saut d'une orbite à une autre se fait en absorbant ou en émettant une quantité déterminée d'énergie (quantum).
Le modèle de Bohr, décomposant l'atome en deux parties, un noyau et un nuage d'électrons, est plus précis que le modèle des sphères dures, pour lequel la surface de la sphère correspond à l'orbite des électrons extérieurs.
Cependant, il présente le gros inconvénient des modèles planétaires : des électrons en orbite autour du noyau sont des charges accélérées, ils devraient rayonner de l'énergie,… et devraient donc venir s'écraser sur le noyau. Le modèle n'explique pas non plus la forme des molécules.
Le modèle actuel : modèle de Schrödinger [modifier]
La naissance de la mécanique ondulatoire de Louis de Broglie 1924, généralisée par Erwin Schrödinger en 1926 amène à proposer un nouveau modèle, dont les aspects relativistes furent décrits par Paul Dirac en 1928 ; il permet d'expliquer la stabilité de l'atome et la description des termes spectroscopiques.
Dans ce modèle, les électrons ne sont plus des billes localisées en orbite, mais des nuages de probabilité de présence. Ce point de vue, révolutionnaire, peut choquer en première approche. Cependant la représentation que l'on pouvait se faire d'un électron — une petite bille ? — était dictée par les formes observées dans le monde macroscopique, transposées sans preuves dans le monde microscopique. Il faut bien se pénétrer du fait que ce que l'on connaît de l'électron ne repose que sur des manifestations indirectes : courant électrique, tube cathodique (télévision)…
Depuis les années 1930, on modélise ainsi l'électron par une « fonction d'onde » dont le carré de la « norme représente la densité de probabilité de présence ». Pour représenter fidèlement les propriétés de l'électron, on ne dispose que des fonctions mathématiques compliquées. Cette abstraction rebute encore bien des physiciens. Nous allons essayer de donner une image de cette notion de fonction d'onde, image nécessairement imparfaite.
- Imaginons que hors de l'atome, l'électron soit une petite bille. Lorsque l'électron est capturé par l'atome, il se « dissout » et devient un nuage diffus, il s'« évapore ». Quand on l'arrache de l'atome, il redevient une petite bille, il se « recondense ». Il existe d'autres exemples d'objet qui changent de forme, par exemple, hors de l'eau, le sel est sous forme de cristaux ; mis dans l'eau, il se dissout, et si l'on fait s'évaporer l'eau, on retrouve des cristaux. Le sel change de forme (cristal compact ou dissous dans l'eau), mais on a tout le temps du sel.
De manière un peu plus exacte : un électron, hors d'un atome, est représenté par un paquet d'ondes, qui peut être considéré, dans certaines limites, comme une petite bille. La mécanique quantique démontre qu'un tel paquet d'ondes s'étale au cours du temps ; au contraire, un électron d'un atome conserve la structure de la fonction d'onde associée à l'orbite qu'il occupe (tant qu'il n'est pas éjecté de l'atome). La mécanique quantique postule donc, non la conservation de la forme (non connue) de l'électron, mais l'intégrale de la probabilité de présence.
Dans le modèle de Schrödinger, les nuages correspondant aux différents électrons s'interpénètrent ; il n'est pas question de se donner une représentation individuelle des électrons chacun sur son orbite, comme cela était dans le cas du modèle de Bohr. Cela est d'autant plus vrai que les électrons sont des particules identiques indiscernables. Les effets d'échange amènent à considérer que chaque électron de l'atome est à la fois sur chaque orbitale occupée (correspondant à une configuration électronique donnée). L'ionisation de l'atome (l'arrachement d'un électron de l'atome) peut alors être représentée par le schéma simplifié ci-dessous.
Pour éviter des complications inutiles, on considérera l'atome le plus simple afin de montrer quelques schémas dévoilant les points fondamentaux du modèle :
- le nuage électronique associé à l'état fondamental, révélant (comme d'autres états) la possibilité pour l'électron d'être au sein du noyau, ce qui a des conséquences en physique nucléaire : capture électronique.
- le nuage électronique associé à une combinaison linéaire de deux orbitales associées au premier niveau excité. Cet exemple montre la possibilité d'obtenir des nuages électroniques pointant vers l'extérieur de l'atome… nous sommes ainsi préparés aux liaisons moléculaires.
Soit ρ(r,θ,φ) la densité de probabilité de présence au point de coordonnées sphériques (r,θ,φ). Pour l'état fondamental, la densité de probabilité, ρ, est maximale au centre de l'atome. Considérons maintenant la densité radiale de probabilité de présence (à la distance r du noyau, toutes les directions confondues) :
 ,
,
cette densité radiale est maximale pour r = r1 de la première orbite du modèle de Bohr (dans l'expression ci-dessus, on a tenu compte de la symétrie sphérique de ρ, identique pour toutes les directions). on a en fait :
- ρ(0,0,0) > ρ(r1,0,0), mais P(0) < P(r1).

En fonction de l'état quantique de l'électron (fondamental, excité …) ces nuages peuvent prendre différentes formes, qui sont décrites en particulier par les harmoniques sphériques. La forme la plus simple est la symétrie sphérique, montrée en particulier, ci-dessus, dans le cas de l'état fondamental, |1s>.
Des combinaisons linéaires de fonctions d'onde, utilisant des harmoniques sphériques distinctes, permettent l'apparition d'une anisotropie qui va devenir essentielle pour le passage de la notion d'atome à celle de molécule. Le schéma ci-contre montre une coupe de la densité de probabilité de présence de l'orbitale hybride |2spz > de l'atome d'hydrogène, coupe contenant Oz axe de symétrie de l'orbitale atomique. Pour cet exemple, l'axe Oz devient une direction privilégiée, mais de plus la densité de probabilité de présence s'étale plus loin pour une orientation donnée.
Ce modèle permet d'expliquer :
- la stabilité de l'atome, les charges sont accélérées, mais elles sont contraintes par la mécanique quantique (relations d'incertitude) ;
- la forme des molécules : orientation préférentielle des nuages électroniques ;
- l'organisation des cristaux : le nuage électronique se comporte comme une coquille dure ;
- les effets spectroscopiques (la quantification des échanges d'énergie) : le nuage ne peut prendre que des formes déterminées, notamment en ce qui concerne la distance r1 du maximum de densité au noyau.
On notera pour terminer que des corrections relativistes sont à apporter, dans le cas des atomes de numéro atomique élevé, pour la détermination des niveaux internes (les vitesses des électrons sur les orbites du modèle de Bohr sont alors importantes).
Le noyau atomique [modifier]
Si la mécanique quantique permit d'expliquer rapidement les caractéristiques spectroscopiques des atomes et des molécules, le cœur de l'atome, son noyau, fut plus difficile à comprendre. Les difficultés sont ici de deux ordres : l'une correspondant à l'importance de l'énergie des particules sondes permettant d'atteindre les dimensions de l'ordre du fermi, l'autre à la nécessaire invention d'au moins une interaction supplémentaire permettant la stabilité d'un noyau constitué de protons (qui se repoussent électriquement) et de neutrons.
Cette compréhension de la cohésion du noyau devait aussi expliquer les phénomènes de radioactivité alpha, bêta et gamma, dont les premières observations dataient de la dernière décennie du XIXe siècle.
La décennie qui précéda la Seconde Guerre mondiale mena à la découverte des deux interactions maîtresses de la stabilité du cœur : l'interaction forte et l'interaction faible. La petitesse de la portée de ces deux interactions, respectivement 10-15 m et 10-18 m explique les difficultés expérimentales rencontrées. Les difficultés théoriques ne manquent pas, non plus ; il ne s'agit pas de lois physiques aussi simples que celles de l'électromagnétisme, même compliquées par la mécanique quantique, mais de la compréhension de toutes les particules élémentaires… L'invention des quarks et des gluons donne ainsi la vision actuelle de l'interaction qui maintient ensemble les nucléons.
Cette physique nucléaire mène aussi à l'explication de la nucléosynthèse, expliquant les aspects nucléaires tableau de Mendeleïev. On se retrouve là dans le foisonnement de la naissance de l'univers et de la dynamique des étoiles.
Notation [modifier]
Un atome est couramment désigné par son symbole chimique, complété par son nombre de masse A (égal au nombre de nucléons de l'atome) placé en haut et à gauche du symbole.
Exemple: le carbone 12 de nombre de masse 12 est noté 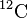 .
.
Il est d'usage de compléter cette écriture par le numéro atomique Z , placé en bas et à gauche du symbole, pour décrire une réaction nucléaire dans laquelle intervient un isotope.
Le carbone 12 est ainsi noté  .
.
Ainsi, le carbone 14  et le carbone 12
et le carbone 12  sont deux isotopes.
sont deux isotopes.
Notes [modifier]
- ↑ Cette notion avait déjà été énoncée dans l'Antiquité, par Anaxagore de Clazomène, et elle fut acceptée par un grand nombre de philosophes (épicuriens, stoïciens, etc.) ; ce principe se fondait sur les observations possibles pour l'époque et fut élaborée selon une démarche scientifique.
Voir aussi [modifier]
Articles connexes [modifier]
- Nucléosynthèse
- Réaction chimique
- Réaction nucléaire
- Règle de l'octet
- Règle du duet
- Orbitale atomique
- Atome d'hydrogène
- Raie à 21 centimètres
Bibliographie [modifier]
- Physics of the atom par M. Russell Wehr et James A. Richards, Jr., chez Addison-Wesley Pubishing Company.
Liens externes [modifier]