Table des constantes astrophysiques

Le tableau suivant contient les valeurs des constantes et paramètres couramment utilisés en astrophysique et aussi plus particulièrement en cosmologie. Concernant les paramètres cosmologiques, le modèle ΛCDM qui est à la base du modèle standard de la cosmologie est utilisé et les valeurs numériques correspondent au meilleur ajustement dans un intervalle de confiance de 68 % (sauf mention explicite).

Ces valeurs sont rassemblées dans la revue annuelle du Particle Data Group.

Dernière mise à jour : 17 juillet 2006.

Quantité	Symbole, équation	Valeur	Commentaire
Vitesse de la lumière dans le vide	$c$	299 792 458 m.s^-1	^[1]
Constante newtonienne de la gravitation	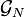$\mathcal{G}_N$	6,673 84(80)×10^-11 m³.kg^-1.s^-2	^[2]
Unité astronomique (constante)	$au$	149 597 870 700 m	^[3]
Année tropique (d'équinoxe à équinoxe)	année	31 556 925,2 s
Année sidérale (d'étoile fixe à étoile fixe)		31 558 149,8 s
Jour sidéral moyen		23h 56m 04,090 53s
Jansky	$J_y$	10^-26 W.m^-2 Hz^-1
Masse de Planck	$\sqrt{\frac{\hbar c}{\mathcal{G}_N}}$	12,209 0(9)×10¹⁸ GeV/c² = 21,764 5(16)×10^-9 kg
Longueur de Planck	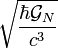$\sqrt{\frac{\hbar \mathcal{G}_N }{ c^3}}$	1,616 24(12)×10^-35 m
Temps de Planck	$\sqrt {\frac{\hbar \mathcal{G}_N}{c^5}}$	5,391 21×10^-44 s
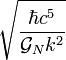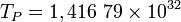Température de Planck	$\sqrt {\frac {\hbar c^5} {\mathcal{G}_N k^2} }$	$T_P = 1,416\ 79\times 10^{32}$ K
Constante de Hubble actuelle	$H_0$	100 h.km.s^-1.Mpc^-1 = h×(9,778 13 Ga)^-1
Constante de Hubble normalisée	$h$	0,73^+0,04_−0,03
Longueur de Hubble	$\frac{c}{H_0}$	≈ 120×10²¹ km
Parsec (1 UA / 1 arc sec)	$pc$	30,856 775 814 672×10¹² km = 3,26... al
Année-lumière	$al$	0,306 6...pc = 9,461...×10¹² km
Rayon de Schwarzschild du Soleil	$\frac{2\mathcal{G}_N M_\odot}{c^2}$	2,95 325 008 km
Masse du Soleil	$M_\odot$	1,988 44(30)×10³⁰ kg
Rayon équatorial du Soleil	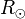$R_\odot$	696 100 km
Luminosité du Soleil	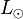$L_\odot$	(384,6±0,8)×10²⁴ W
Rayon de Schwarzschild de la Terre	$\frac{2\mathcal{G}_N M_\oplus}{c^2}$	8,870 056 22 mm
Masse de la Terre	$M_\oplus$	5,972 3(9)×10²⁴ kg
Rayon équatorial moyen de la Terre	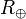$R_\oplus$	6,378 140×10⁶ m
Vitesse du Soleil autour du centre de la Voie lactée	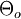$\Theta_o$	220(20) km.s^-1
Distance du Soleil au centre galactique	$R_o$	8,0(5) kpc
Densité locale du disque galactique	$\rho_{disque}$	3-12×10^-24 g.cm^-3 ⋍ 2-7 GeV/c².cm^-3
Densité locale du halo galactique	$\rho_{halo}$	2-13×10^-25 g.cm^-3 ⋍ 0,1-0,7 GeV/c²).cm^-3
Température actuelle du CMB	$T_0$	2,725±0,001 K
Amplitude dipolaire actuelle du CMB		3,346±0,017 mK
Vitesse du Soleil par rapport au CMB		369±2 km.s^-1 en direction de (l,b) = (263,86°±0,04°, 48,24°±0,010°)
Vitesse du groupe local par rapport au CMB	$v_{LG}$	627±22 km.s^-1 en direction de (l,b) = (276°±3°, 30°±3°)
Constante de Boltzmann (ou densité d'entropie)	$s/k$	2889,2 (T/2,725)³.cm^-3
Densité de photons du CMB	$n_\gamma$	410,5±0,5 cm^-3
Facteur d'échelle pour la constante cosmologique	$\frac{c^2}{3 H_0^2}$	2,853×10⁵¹ h^-2.m²
Densité massique critique de l'univers	$\rho_c = \frac{3H_0^2}{8\pi\mathcal{G}_N}$	$\begin{matrix}2,775 366 27 \times 10^{11} h^2.M_{\odot}.Mpc^{-3}\\ = 1,878 37(28) \times 10^{-29}h^2.g.cm^{-3}\\ = 1,053 69 (16)\times 10^{-5} h^2.(GeV/c^2).cm^{-3}\end{matrix}$	quantité dérivée
Densité de la matière sans pression dans l'univers	$\Omega_m=\frac{\rho_m}{\rho_c}$	0,127^+0,007_−0,009h^-2 ⇒ 0,24^+0,03_−0,04
Densité de baryons dans l'univers	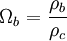$\Omega_b=\frac{\rho_b}{\rho_c}$	0,0223^+0,0007_−0,0009h^-2 ⇒ 0,042^+0,003_−0,005
Densité de matière sombre dans l'univers	$\Omega_{dm}=\Omega_m-\Omega_b$	0,105^+0,007_−0,010h^-2 ⇒ 0,20^+0,02_−0,04
Densité de rayonnement dans l'univers	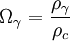$\Omega_\gamma=\frac{\rho_\gamma}{\rho_c}$	(2,471±0,004)h×10^-5 h^-2 ⇒ (4,6±0,5)×10^-5
Densité de neutrinos dans l'univers	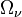$\Omega_\nu$	< 0,007 h^-2 ⇒ < 0,014 (à 95 % de niveau de confiance)
Densité d'énergie sombre dans l'univers	$\Omega_\Lambda$	0,76^+0,04_−0,06
Densité d'énergie totale dans l'univers	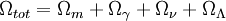$\Omega_{tot}=\Omega_m+\Omega_\gamma+\Omega_\nu+\Omega_\Lambda$	1,003^+0,013_−0,017
Rapport baryons/photons	$\eta=\frac{n_b}{n_\gamma}$	4,7×10^-10 < η < 6,5×10^-10 (95 %)
Densité de nombre de baryons	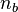$n_b$	(1,9×10^-7 < n_b < 2,7×10^-7)cm^-3
Paramètre d'équation d'état pour l'énergie sombre	$w$	-0,97^+0,07_−0,09
Fluctuation d'amplitude à l'échelle 8 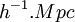$h^{-1}.Mpc$	$\sigma_8$	0,74^+0,05_−0,06
Indice spectral scalaire de l'ajustement de la loi de puissance aux observations	$n_s$	0,951^+0,015_−0,019
Variation de l'indice spectral pour 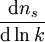$k_0=0.05 Mpc^{-1}$	$\frac{{\rm d} n_s}{{\rm d}\ln k}$	-0,055^+0,029_−0,035
Rapport des perturbations tensorielles/scalaires dans le CMB pour $k_0=0.05 Mpc^{-1}$	$r=\frac{T}{S}$	< 0,55 (95 %)
Profondeur optique de réionisation	$\tau$	0,09±0,03
Âge de l'univers	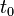$t_0$	13,7^+0,1_−0,2 Ga