PREUVE OVNI

Fille de l'ancienne théorie des quanta, la mécanique quantique constitue le pilier d'un ensemble de théories physiques qu'on regroupe sous l'appellation générale de physique quantique. Cette dénomination s'oppose à celle de physique classique, celle-ci échouant dans sa description du monde microscopique — atomes et particules — ainsi que dans celle de certaines propriétés du rayonnement électromagnétique.

Les principes fondamentaux de la mécanique quantique ont été établis essentiellement entre 1922 et 1927 par Bohr, Dirac, de Broglie, Heisenberg, Jordan, Pauli et Schrödinger. Ils permettent une description complète de la dynamique d'une particule massive non relativiste. Bohr a proposé une interprétation du formalisme, appelée interprétation de Copenhague, fondée sur le principe de correspondance.

Les principes de base ont été complétés par Bose et Fermi afin d'autoriser la description d'un ensemble de particules identiques, ouvrant la voie au développement d'une physique statistique quantique. Enfin, en 1930, le mathématicien Von Neumann a précisé le cadre mathématique rigoureux de la théorie.

Son extension relativiste pertinente est la théorie quantique des champs.

Sommaire

[masquer]

Panorama général [modifier]

Introduction [modifier]

Fille de l'ancienne théorie des quanta, la mécanique quantique fixe un cadre mathématique tout à fait cohérent qui a permis de remédier à tous les désaccords entre certains résultats expérimentaux mis en évidence à la fin du XIX^e siècle et les prédictions théoriques correspondantes de la physique classique.

La mécanique quantique a repris et développé l'idée de dualité onde-corpuscule introduite par de Broglie en 1924 consistant à considérer les particules de matière non pas seulement comme des corpuscules ponctuels, mais aussi comme des ondes, possédant une certaine étendue spatiale (voir la mécanique ondulatoire). Bohr a introduit le concept de complémentarité pour résoudre cet apparent paradoxe : tout objet physique est bien à la fois une onde et un corpuscule, mais ces deux aspects, mutuellement exclusifs, ne peuvent être observés simultanément^[1]. Si l'on observe une propriété ondulatoire, l'aspect corpusculaire disparaît. Réciproquement, si l'on observe une propriété corpusculaire, l'aspect ondulatoire disparaît.

A ce jour, aucune contradiction n'a pu être décelée entre les prédictions de la mécanique quantique et les tests expérimentaux associés. Ce succès a hélas un prix : la théorie repose sur un formalisme mathématique abstrait, qui rend son abord assez difficile pour le profane.

Quelques exemples de succès [modifier]

Historiquement, la théorie a d'abord permis de décrire correctement les structures électroniques des atomes et des molécules, ainsi que leurs interactions avec un champ électromagnétique. Elle permet également d'expliquer le comportement de la matière condensée, notamment : la structure des cristaux et leurs vibrations (appelées phonons), les propriétés de conductivité électrique et de conduction thermique des métaux grâce à la théorie des bandes, l'existence et les propriétés des semi-conducteurs, l'effet tunnel. Elle permet enfin de comprendre les supraconducteurs et les superfluides.

Un autre grand succès de la mécanique quantique fut de résoudre le paradoxe de Gibbs : en physique statistique classique, des particules identiques sont considérées comme étant discernables, et l'entropie n'est alors pas une grandeur extensive. L'accord entre la théorie et l'expérience fut rétabli en tenant compte du fait que des particules identiques sont indiscernables en mécanique quantique.

La théorie quantique des champs, généralisation relativiste de la mécanique quantique, permet quant à elle de décrire les phénomènes où le nombre total de particules n'est pas conservé : radioactivité, fission nucléaire (c'est-à-dire la désintégration du noyau atomique) et fusion nucléaire.

Quantification canonique [modifier]

Onde plane classique [modifier]

En physique classique, une onde plane progressive monochromatique de pulsation $ω$ se propageant dans la direction des x positifs s'écrit :

$\Psi(x,t) = \Psi_{0} \ e^{-i(\omega t - k x)}$

où l'amplitude $Ψ 0$ est une certaine constante. Si nous introduisons dans cette expression classique les relations quantiques de Broglie, nous pouvons faire apparaître les grandeurs énergie E et impulsion p :

$\Psi(x,t)\ = \ \Psi_{0} \ e^{-i({\frac{E}{\hbar}t-\frac{p_x}{\hbar}x})}$

Cette expression se généralise facilement en dimension 3 :

$\Psi(\vec{r},t)\ = \ \Psi_{0} \ e^{-\frac{i}{\hbar}(Et-\vec{p}\cdot\vec{r})}$

Il est alors clair que si l'on veut obtenir l'énergie, il suffit de dériver par rapport au temps :

$i \ {\hbar} \ \frac{{\partial}\Psi}{{\partial}t} \ = \ E \ \Psi(\vec{r},t)$

et que pour obtenir l'impulsion, on doit prendre le gradient :

$- \ i \ {\hbar} \ {\nabla}\Psi \ = \ \vec{p} \ \Psi(\vec{r},t)$

Règles de la quantification canonique [modifier]

La quantification canonique consiste à remplacer les variables dynamiques classiques de position et d'impulsion, qui sont des nombres réels, par des opérateurs, selon les règles de substitution suivantes :

à la coordonnée de position $x i$ est associé un opérateur de position $\hat{x}^i$ tel que :

$\hat{x}^i \ f(\vec{r}) \ = \ x^i \ f(\vec{r})$

à la variable d'impulsion $p i$ est associée un opérateur impulsion $\hat{p}_i$ tel que :

$\hat{p}_i \ f(\vec{r}) \ = \ - \ i \ {\hbar} \ \frac{\partial f(\vec{r})}{\partial x^i}$ , soit : $\hat{p}_i \ = \ - \ i \ {\hbar} \ \frac{\partial}{\partial x^i}$

à la variable énergie est associé l'opérateur de dérivation temporelle :

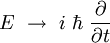
$E \ f(\vec{r}, t ) \ = \ i \ {\hbar} \ \frac{\partial f(\vec{r}, t )}{\partial t}$ , soit : $E \ \to \ i \ {\hbar} \ \frac{{\partial}}{{\partial}t}$

Équation de Schrödinger [modifier]

Article détaillé : Équation de Schrödinger.

Dérivation heuristique de l'équation [modifier]

Le hamiltonien donnant l'énergie mécanique totale d'une particule massive non relativiste soumise à une force dérivant d'un potentiel est donné par l'expression classique :

$H(\vec{r}, \, \vec{p}) \ = \ \frac{p^2}{2m} \ + \ V(\vec{r}) \ = \ E$

Cette grandeur contient toute l'information nécessaire à l'étude classique de l'évolution dynamique du système via les équations canoniques de Hamilton, moyennant la donnée d'une condition initiale. A cette particule classique est associée une onde $\Psi(\vec{r},t)$ , dont on cherche l'équation d'évolution. D'après les règles de la quantification canonique, le Hamiltonien classique devient un opérateur :

$\hat{H} \ = \ \frac{\hat{p}^2}{2m} \ + \ V(\hat{r}) \ = \ - \ \frac{\hbar^2}{2m} \ \vec{\nabla}^2 \ + \ V(\vec{r})$

L'opérateur différentiel $\vec{\nabla}^2$ est l'opérateur Laplacien : $\Delta = \vec{\nabla}^2$ . L'équation classique de conservation de l'énergie :

$H(\vec{r}, \, \vec{p}) \ = \ E$

donne, en multipliant de chaque coté par la fonction d'onde, l'équation de Schrödinger dépendante du temps :

$- \ \frac{\hbar^2}{2m} \ \Delta \ \Psi(\vec{r},t) \ + \ V(\vec{r}) \ \Psi(\vec{r},t) \ = \ i \ {\hbar} \ \frac{{\partial}\Psi(\vec{r},t)}{{\partial}t}$

Rappelons que cette équation n'est valable que pour des vitesses classiques petites devant la vitesse de la lumière dans le vide.

Interprétation physique de la fonction d'onde [modifier]

L'interprétation physique de la fonction d'onde $Ψ$ sera donnée par Born en 1926 : le module au carré de cette fonction d'onde $\left| \Psi \right|^2 = \overline{\Psi} \Psi$ représente la densité de probabilité de présence de la particule considérée, c'est-à-dire que :

$dP(\vec{r},t) \ = \ \left| \Psi(\vec{r},t) \right|^2 \ dV$

s'interprète comme étant la probabilité de trouver la particule dans un petit volume $d V$ situé au voisinage du point 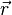$\vec{r}$ de l'espace à l'instant $t$ . En particulier, la particule étant nécessairement située quelque part dans l'espace entier, on a la condition de normalisation :

$\iiint dP(\vec{r},t) \ = \ \iiint \left| \Psi(\vec{r},t) \right|^2 \ dV \ = \ 1$

Remarque : cette interprétation statistique pose un problème lorsque le système quantique étudié est l'Univers entier, comme en cosmologie quantique. Dans ce cas, les physiciens théoriciens utilisent préférentiellement l'interprétation dite des « mondes multiples » d'Everett.

Méthodes de résolution [modifier]

En dehors de quelques cas particuliers où on sait l'intégrer exactement, l'équation de Schrödinger ne se prête en général pas à une résolution analytique exacte. Il faut alors :

soit développer des techniques d'approximations comme la théorie des perturbations.

soit la résoudre numériquement. Cette résolution numérique permet notamment de visualiser la disposition curieuse des orbitales électroniques.

Formalisme de Dirac : bras, kets, et postulats fondamentaux [modifier]

Article détaillé : Notation bra-ket.

Dirac a introduit en 1925 une notation puissante^[2], dérivée de la théorie mathématique des formes linéaires sur un espace vectoriel. Dans ce formalisme abstrait, les postulats de la mécanique quantique prennent une forme concise et particulièrement élégante.

Mécanique quantique & relativité [modifier]

Article détaillé : Théorie quantique des champs.

La mécanique quantique est une théorie non relativiste : elle n'incorpore pas les principes de la relativité restreinte d'Einstein. En appliquant les règles de la quantification canonique à la relation de dispersion relativiste, on obtient l'équation de Klein-Gordon (1926). Les solutions de cette équation présentent toutefois de sérieuses difficultés d'interprétation dans le cadre d'une théorie censée décrire une seule particule : on ne peut notamment pas construire une densité de probabilité de présence partout positive, ce qui est lié au fait que l'équation de Klein-Gordon contient une dérivée temporelle seconde. Dirac cherchera alors une autre équation relativiste du premier ordre en temps, et obtiendra l'équation de Dirac, qui décrit très bien les fermions de spin un-demi comme l'électron.

Le cadre pertinent pour interpréter toutes les équations quantiques relativistes sans difficultés est la théorie quantique des champs.

L'équation de Dirac incorpore naturellement l'invariance de Lorentz avec la mécanique quantique ainsi que l'interaction avec le champ électromagnétique mais qui est traité encore de façon classique (on parle d'approximation semi-classique). Elle constitue la mécanique quantique relativiste. Mais du fait précisément de cette interaction entre les particule et champ il est alors nécessaire, afin d'obtenir une description cohérente de l'ensemble, d'appliquer la procédure de quantification également au champ électromagnétique. Le résultat de cette procédure est l'électrodynamique quantique dans laquelle l'unité entre champ et particule est encore plus transparente puisque désormais la matière elle aussi est décrite par un champ. L'électrodynamique quantique est un exemple particulier de théorie quantique des champs. D'autre théories quantique des champs ont été développées par la suite au fur et à mesure que les autres interactions fondamentales ont été découvertes (théorie électrofaible puis chromodynamique quantique).

Les inégalités de Heisenberg [modifier]

Article détaillé : Principe d'incertitude.

Les relations d'incertitude de Heisenberg traduisent l'impossibilité de préparer un état quantique correspondant à des valeurs précises de certains couples de grandeurs conjuguées. Ceci est lié au fait que les opérateurs quantiques associés à ces grandeurs classiques ne commutent pas.

Inégalité position-impulsion [modifier]

Considérons par exemple la position $x\,$ et l'impulsion $p_x\,$ d'une particule. En utilisant les règles de la quantification canonique, il est facile de vérifier que les opérateurs de position et d'impulsion vérifient :

$\left[ \hat{x}^i , \hat{p}_j \right] f( \vec{r} ) \ = \ \left( \hat{x}^i \hat{p}_j - \hat{p}_j \hat{x}^i \right) f( \vec{r} ) \ = \ i \hbar \ \delta^i_j \ f( \vec{r} )$

La relation d'incertitude est définie à partir des écarts quadratiques moyens de grandeurs conjuguées. Dans le cas de la position $x$ et de l'impulsion $p x$ d'une particule, elle s'écrit par exemple :

${\Delta}x \, \cdot \, {\Delta}p_x \ {\ge} \ \frac{\hbar}{2}$

Plus l'état possède une distribution resserrée sur la position, plus sa distribution sur les valeurs de l'impulsion qui lui est associée est large. Cette propriété rappelle le cas des ondes, via un résultat de la transformée de Fourier, et exprime ici la dualité onde-corpuscule. Il est clair que ceci mène à une remise en cause de la notion classique de trajectoire comme chemin continu différentiable^[3].

Inégalité temps-énergie [modifier]

Il existe également une relation d'incertitude portant sur l'énergie d'une particule et la variable temps. Ainsi, la durée 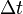$\Delta t\,$ nécessaire à la détection d'une particule d'énergie 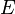$E\,$ à $\Delta E\,$ près^[4] vérifie la relation :

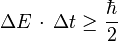
${\Delta}E \, \cdot \, {\Delta}t \ {\ge} \ \frac{\hbar}{2}$

Cependant, la dérivation de cette inégalité énergie-temps est assez différente de celle des inégalités position-impulsion^[5].

En effet, si le Hamiltonien est bien le générateur des translations dans le temps en mécanique hamiltonienne, indiquant que temps et énergie sont conjuguées^[6], il n'existe pas d'opérateur temps en mécanique quantique (« théorème » de Pauli), c'est-à-dire qu'on ne peut pas construire d'opérateur $\hat{T}$ qui obéirait à une relation de commutation canonique avec l'opérateur Hamiltonien $\hat{H}$ :

$\left[ \hat{H} , \hat{T} \right] \ = \ i \hbar \ \hat{1}$

ceci pour une raison très fondamentale : la mécanique quantique a en effet été inventée pour que chaque système physique stable possède un état fondamental d'énergie miminum. L'argument de Pauli est le suivant : si l'opérateur temps existait, il posséderait un spectre continu. Or, l'opérateur temps, obéissant à la relation de commutation canonique, serait aussi le générateur des translations en énergie. Ceci entraîne alors que l'opérateur hamiltonien posséderait lui aussi un spectre continu, en contradiction avec le fait que l'énergie de tout système physique stable se doit d'être bornée inférieurement ^[7].

L'intrication [modifier]

Article détaillé : intrication quantique.

Définition [modifier]

L'intrication est un état quantique (voir aussi fonction d'onde) décrivant deux systèmes classiques (ou plus) non factorisable en un produit d'états correspondant à chaque système classique.

Deux systèmes ou deux particules peuvent être intriqués dès qu'il existe une interaction entre eux. En conséquence, les états intriqués sont la règle plutôt que l'exception. Une mesure effectuée sur l'une des particules changera son état quantique selon le postulat quantique de la mesure. Du fait de l'intrication, cette mesure aura un effet simultané sur l'état de l'autre particule. Néanmoins, il est incorrect d'assimiler ce changement d'état à une transmission d'information plus rapide que la vitesse de la lumière (et donc une violation de la théorie de la relativité). La raison est que le résultat de la mesure de la première particule est toujours aléatoire dans le cas d'états intriqués. Il est donc impossible de « transmettre » quelqu'information que ce soit puisque la modification de l'état de l'autre particule, pour immédiate qu'elle soit, n'en reste pas moins tout aussi aléatoire. Les corrélations entre les mesures des deux particules, bien que très réelles et mises en évidence dans de nombreux laboratoires de par le monde, restent indétectables tant que les résultats des mesures ne sont pas comparés, ce qui implique nécessairement un échange d'information classique, respectueux de la relativité (voir aussi le Paradoxe EPR). La téléportation quantique fait usage de l'intrication pour assurer le transfert de l'état quantique d'un système physique vers un autre système physique. Ce processus est le seul moyen connu de transférer parfaitement l'information quantique. Il ne peut dépasser la vitesse de la lumière et est également « désincarné », en ce sens qu'il n'y a pas de transfert de matière (contrairement à la téléportation fictive de Star Trek).

Cet état ne doit pas être confondu avec l'état de superposition. Un même objet quantique peut avoir deux (ou plus) états superposés. Par exemple un même photon peut être dans l'état "polarité longitudinale" et "polarité transversale" simultanément. Le chat de Schrödinger est simultanément dans l'état "mort" et "vivant". Un photon qui passe une lame semi-réfléchissante est dans l'état superposé "photon transmis" et "photon réfléchi". C'est uniquement lors de l'acte de mesure que l'objet quantique possédera un état déterminé.

Dans le formalisme de la physique quantique, un état d'intrication de plusieurs objets quantique est représenté par un produit tensoriel des vecteurs d'état de chaque objet quantique. Un état de superposition ne concerne qu'un seul objet quantique (qui peut être une intrication), et est représentée par une combinaison linéaire des différentes possibilités d'états de celui-ci.

Téléportation quantique [modifier]

Article détaillé : Téléportation quantique.

On ne peut déterminer l'état d'un système quantique qu'en l'observant, ce qui a pour effet de détruire l'état en question. Celui-ci peut en revanche, une fois connu, être en principe recréé ailleurs. En d'autres termes, la duplication n'est pas possible dans le monde quantique, seule l'est une reconstruction en un autre endroit, voisine du concept de téléportation dans la science-fiction.

Elaborée théoriquement en 1993 par C.H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres, et W. Wootters dans l'article Teleporting an unkown quantum state by dual classical and EPR channels, de la Physical Review Letter, cette reconstruction a été réalisée expérimentalement en 1997, sur des photons, par l'équipe d'Anton Zeilinger à Innsbruck, et plus récemment sur des atomes d'hydrogène.

16/09/2007

0 J'aime 0 Poster un commentaire

A découvrir aussi

Retour aux articles de la catégorie * Physique NUCLEAIRE et QUANTIQUE -

⨯

Inscrivez-vous au blog

Soyez prévenu par email des prochaines mises à jour

Rejoignez les 525 autres membres

PREUVE OVNI

Articles

Album photos

Forum

Membres

A découvrir

Statistiques

Mécanique quantique - Partie 1

Mécanique quantique

Un article de Wikipédia, l'encyclopédie libre.