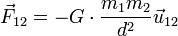En poursuivant votre navigation sur ce site, vous acceptez l'utilisation de cookies pour vous proposer des services et offres adaptés à vos centres d'intéréts.

Gravitation

 

Gravitation

Un article de Wikipédia, l'encyclopédie libre.
Aller à : Navigation, rechercher
Page d'aide sur l'homonymie Pour les articles homonymes, voir Gravitation (homonymie).

La gravitation est le phénomène d'interaction physique qui cause l'attraction réciproque des corps massifs entre eux, sous l'effet de leur masse. Il s'observe en raison de l'attraction terrestre qui nous retient au sol, qui se nomme la gravité et qui est responsable de plusieurs manifestations naturelles : les marées, l'orbite des planètes autour du Soleil, la sphéricité de la plupart des corps célestes en sont quelques exemples. D'une manière plus générale, la structure à grande échelle de l'univers est déterminée par la gravitation.

Plusieurs théories ont tenté de rendre compte de la gravitation. Aujourd'hui, la théorie de la relativité générale d'Albert Einstein, proposée en 1915, est celle qui décrit toutes les observations faites en astronomie ainsi qu'en cosmologie. La loi de la gravitation de Newton, élaborée à la fin du XVIIe siècle, demeure cependant une excellente approximation dans la plupart des cas (vitesses faibles par rapport à celle de la lumière), et on l'utilise donc encore aujourd'hui pour sa simplicité.

Aux échelles microscopiques, la gravitation est la plus faible des quatre interactions fondamentales de la physique ; elle devient dominante au fur et à mesure que les échelles de grandeur augmentent. Avec la force électromagnétique, elle est la seule à agir au-delà de la dimension du noyau atomique. De plus, comme elle est toujours attractive elle domine sur les forces électromagnétiques qui tendent à se compenser, étant tantôt attractives, tantôt répulsives.

Elle est toujours l'objet de nombreuses recherches et la communauté scientifique considère qu'élaborer une théorie plus complète de la gravitation, capable de prendre en compte les effets de nature microscopique (quantiques), et pour cette raison appelée gravitation quantique, est un des grands défis à relever pour la physique du XXIe siècle.

La gravitation maintient les planètes en orbite autour du Soleil. (Échelle non respectée.)

Compréhension intuitive[modifier | modifier le code]

Penser, comme Aristote, que sur Terre (et avec l'hypothèse du vide atmosphérique) plus un corps est lourd, plus il tombe vite c'est faire une confusion entre quantité et qualité :

  1. Quantité : prenons en main un corps attiré par la Terre, et décomposons-le, par une vue de l'esprit, en une myriade de « micro briques de matière ». Chaque « brique de matière », étant attirée par la Terre, exerce une force, nommée poids, sur la main et le grand nombre de briques exerçant ce poids donne le poids global. Le poids global d'un objet dépend de la quantité de matière : c'est une notion approximativement extensive.
  2. Qualité : lâchons ce corps (supposé fait d'une seule matière), il tombe. Chaque micro-brique tombe parce qu'elle est attirée par la Terre, seulement à cause de cela et acquiert une certaine vitesse, dépendant de son inertie, sans tenir compte de la présence éventuelle d'autres briques alentour. Donc, quel que soit le nombre de micro-briques, toutes tombent simultanément (car toutes faites de la même matière, donc identiques avec un bon découpage en micro-briques), à la même vitesse : c'est la vitesse du corps entier, qui ne dépend donc pas du nombre de briques et donc ne dépend pas de sa masse. Cette vitesse est une qualité du corps totalement indépendante de la quantité de matière : c'est une notion intensive.

Ainsi, bien qu'elles sont intimement associées dans nos expériences et nos sensations courantes, les deux notions (poids et vitesse de chute) sont bien distinctes.

La distinction ci-dessus entre qualité et quantité n'explique pas qu'en l'absence d'air, du bois et du métal tombent exactement à la même vitesse. Ce fait expérimental laisse penser que ces deux matières différentes (ainsi que toutes les autres) ont en commun la même qualité. Les expérimentations et les réflexions sur ce sujet ont donné le principe d'équivalence.

En termes plus précis, plus complets et surtout plus "scientifiques" que cette introduction très intuitive, la relativité générale étudie la gravitation, et comme « qualité commune » aux corps, dans le problème posé ci-dessus, elle permet de proposer « l'énergie » ; bien qu'en toute rigueur cette théorie admet comme hypothèse l'existence de cette « qualité commune » (en admettant le principe d'équivalence) et qu'elle exclut toute idée d'attraction et de force gravitationnelle.

En laissant tomber simultanément des objets de poids, de formes ou de volumes très différents, par exemple une balle de mousse et une bille de métal de même diamètre, depuis une hauteur d'homme, on peut penser qu'il y a égalité des vitesses de chute[note 1]. Mais, quand la hauteur de chute est plus grande, des différences perceptibles apparaissent, du fait des frottements de l'air. Galilée sera le premier à comprendre que les frottements sont la seule cause des différences de vitesses entre ces corps.

La modélisation de Galilée (1564-1642)[modifier | modifier le code]

Galilée ne se préoccupe guère du problème de la chute dans le vide d'objets de natures différentes : il a déjà beaucoup à faire avec la chute de sphères de métal, des corps graves, sur la terre, elle-même sphérique ; de plus, la notion de vide physique est relativement absente de sa pensée (la découverte de la notion physique de vide par Torricelli, élève de Galilée, n'a lieu qu'en 1644).

Par une expérience du haut de la tour de Pise, il aurait constaté que des balles lourdes et de poids différents ont le même temps de chute, mais, quand il affirme que la vitesse de chute ne dépend pas du poids de l'objet, la raison qu'il expose tient à des expérimentations sur des pendules aux poids différents. Toutefois, On n'a aucune preuve que cette expérience a bien été faite par Galilée[réf. nécessaire].

Article détaillé : Pendule pesant.

Vers 1604, Galilée utilise un constat : quand on lâche un objet, sa vitesse initiale est nulle, mais quand il arrive au sol sa vitesse… n'est pas nulle. Donc la vitesse varie continûment durant la chute ! Galilée propose une loi simple : la vitesse serait proportionnelle au temps écoulé depuis le début de la chute.

Ainsi : vitesse = constante×temps écoulé

Il en conclut, par un calcul qui s'approche du calcul intégral (lequel sera formellement inventé par Isaac Newton et Gottfried Wilhelm von Leibniz près de 80 ans plus tard), en reprenant la démonstration établie plus de deux siècles auparavant par Nicolas d'Oresme, que, pendant une chute, la distance parcourue est proportionnelle au carré du temps écoulé.

Plus précisément : distance = constante×0,5×temps écoulé2

Son idée est confirmée dans une expérience, avec du matériel construit de sa main : une gouttière inclinée le long de laquelle des clochettes sont disposées pour indiquer le passage de la bille.

La constante sera notée g (voir pesanteur) et sa valeur[note 2] déterminée expérimentalement : g = 9,81 m·s−2.

Aujourd'hui, encore cette modélisation reste satisfaisante pour toutes les activités humaines qui se font au niveau du sol de la Terre.

La modélisation d'Isaac Newton (1643-1727)[modifier | modifier le code]

Isaac Newton jette un pont entre ciel et terre. Il suggère que la force qui nous retient au sol est la même que celle qui retient la lune autour de la terre.
Article détaillé : Loi universelle de la gravitation.

Mathématicien autant que physicien, Isaac Newton mit au point, entre 1665 et 1685, sa théorie de la mécanique basée sur l’étude de l’accélération, et non seulement de la vitesse comme le faisaient Galilée et René Descartes.

Loi fondamentale de la dynamique : à partir du principe d’inertie de Descartes (qui étudiait la conservation de la quantité de mouvement), il conclut que la somme des forces qui s’exercent sur un corps est égale à ma, où m est la masse « inertielle » (qui rend difficile la mise en mouvement ou l’arrêt d’un véhicule pouvant se déplacer sans frottement) et a est l’accélération (le rythme de la variation de la vitesse).

Newton chercha à unifier les lois connues pour les objets sur terre et les lois observées pour les astres, notamment la gravitation terrestre et les mouvements des planètes.

En considérant deux corps ponctuels exerçant une force gravitationnelle l’un sur l’autre, une justification de la loi de Newton est la suivante :

  • À partir des lois de Kepler, que celui-ci avait obtenues en observant les mouvements des planètes du Système solaire, et de la loi de Christiaan Huygens sur la force centrifuge, Newton conclut que la force agissante entre deux corps s’exerce en ligne droite entre les deux corps et est proportionnelle à : \frac{1}{d^2}, où d est la distance entre les deux corps.
  • Considérant que cette force est proportionnelle à la quantité de matière présente dans le corps exerçant cette force (un corps ayant deux fois plus de matière exerce une force égale à la somme des forces de deux corps, donc exerce une force deux fois plus grande), il suppose que la force est proportionnelle à m_G, nombre appelé « masse gravifique », proportionnelle à la quantité de matière dans le corps et reflétant sa capacité à exercer cette force (la « charge » gravitationnelle en fait), dépendant sans doute de sa nature (pomme, plomb, argile ou gaz…).
  • En vertu du principe des actions réciproques, la force exercée par l’autre corps sur le premier doit être égale (et de sens opposé) et doit aussi être proportionnelle à m'_G, la masse gravifique du deuxième corps.
  • Aucun autre paramètre ne semblant rentrer en compte, cette force s’exprime sous la forme : F_\frac{A}{B} = G\times\frac{m_a m_b}{d^2} où G est une constante, appelée constante gravitationnelle qui est environ égale à 0,000 000 000 067Nm²kg-²

En écrivant la loi fondamentale de la dynamique, on obtient ma=G\cdot\frac{m_Gm'_G}{d^2}. On constate que pour que l’accélération a (et donc la vitesse) d’un corps en chute libre sur terre soit indépendante de sa masse inertielle (comme l’a expérimenté Galilée), il faut que m=m_G pour ce corps, c’est-à-dire que la « masse gravifique » soit égale à la masse inertielle, indépendamment de la nature du corps (en fait la proportionnalité entre ces masses suffit, avec le même coefficient pour tous les matériaux, ensuite on peut les rendre égales avec un choix des unités de mesure). Newton a testé cette égalité pour de nombreux matériaux, et depuis les expériences n’ont jamais cessé, avec de plus en plus de raffinements (balance d’Eötvös, etc.). Depuis, cette égalité a été appelée le principe d’équivalence faible.

L’action à distance (sans contact, à travers le vide) et la propagation instantanée de la force de gravitation ont aussi suscité des doutes, y compris de Newton.

Dans l’écriture vectorielle moderne, la force gravitationnelle s’écrit :

\vec{F}_{12}=-G\cdot\frac{m_1 m_2}{d^2}\vec{u}_{12}
  • \vec{F}_{12} étant la force gravitationnelle exercée par le corps 1 sur le corps 2 (en newton ou m·kg·s−2) ;
  • G, la constante gravitationnelle, qui vaut 6,6742×10-11 N·m2·kg−2 (ou m3·kg−1·s−2)[note 3] ;
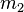  • m_1 et m_2, les masses des deux corps en présence (en kilogrammes) ;
  • d, la distance entre les 2 corps (en mètres) ;
  • \vec{u}_{12} est un vecteur unitaire dirigé du corps 1 vers le corps 2 ;
  • le signe – indique que le corps 2 est attiré par le corps 1.

La loi newtonienne de la gravitation permet de retrouver la loi de Galilée, en première approximation: avec r= rayon terrestre et m_T= masse de la Terre, on a g=G\cdot\frac{m_T}{r^2}=9,81 m·s−2.

La théorie newtonienne est bien vérifiée expérimentalement. D’un point de vue technique, elle suffit pour faire voler des objets plus lourds que l’air et pour envoyer des hommes sur la Lune. La force de pesanteur est la résultante de la force de gravité et de forces axifuges (la force centrifuge liée à la rotation de la terre sur elle-même, de la loi de l’inertie du mouvement, etc.).

Reformulations de la théorie de Newton[modifier | modifier le code]

Joseph-Louis Lagrange a réécrit, à partir de 1762, la théorie de la gravitation et l'ensemble de la physique en y introduisant le principe de moindre action qui avait été formulé par Pierre Louis Maupertuis vers 1744.

William Rowan Hamilton, vers 1830, a substitué au principe de moindre action la notion d'énergie, qui est une constante pour tout système isolé (c’est-à-dire : sans interaction avec l'extérieur) et qui sera de la plus grande importance pour la physique relativiste et en mécanique quantique, au XXe siècle.

L'idée d'un champ de force, introduite par Michael Faraday, ne permit qu'une réécriture de la théorie de la gravitation newtonienne, mais cette notion se révélera féconde quand il s'agira de concevoir la gravitation relativiste. Le champ ou champ de force de la gravitation est une propriété de l'espace due à la masse d'un corps. Une autre masse entrant en contact avec ce champ est soumis à une influence, une force, due au champ. Ainsi, l'influence gravitationnelle n'est pas, dans ce cadre, créée et transportée instantanément d'un corps à l'autre, mais est déjà présente dans tout l'espace sous la forme du champ et à son contact un corps voit sa dynamique modifiée. Toutefois, le champ est lui-même instantanément modifié par le corps qui le crée.

Si M est la masse du corps ponctuel émetteur du champ, et si r est la distance entre ce corps et le point de l'espace que l'on considère, le champ en ce point s'exprime par V(r)=-\frac{G.M}{r}\, , le « potentiel gravitationnel » .

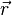Un corps ponctuel de masse m étant en contact avec ce champ, la force qu'il subit est \vec F(r) = -m\vec \nabla V(r) = -\frac{G.M.m}{r^2}.\vec u_{\vec r}, où \vec u_{\vec r} est le vecteur unitaire de même direction et de même sens que \vec r qui va de M à m.

Article détaillé : Champ gravitationnel.

La modélisation d'Albert Einstein (1879-1955)[modifier | modifier le code]

Depuis la relativité générale, la gravitation n'est plus perçue comme une force d'attraction, mais plutôt comme une manifestation de la déformation de la géométrie de l'espace-temps sous l'influence des objets qui l'occupent.
Article détaillé : Introduction à la relativité générale.

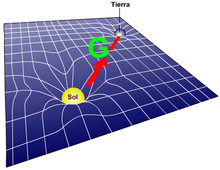
Après avoir énoncé la théorie de la relativité restreinte en 1905, Albert Einstein cherche à la rendre compatible avec la gravitation dont l'effet est supposé se propager à une vitesse infinie dans la théorie de Newton, alors que la vitesse de la lumière est la vitesse maximale pour toute interaction selon la relativité restreinte.

Vers 1915, on émettra l'hypothèse que la gravitation n'est pas une force au sens usuel que l'on donne à ce mot en physique, mais une manifestation de la déformation de l'espace-temps sous l'effet de l'énergie de la matière qui s'y trouve. Cette hypothèse résulte de l'observation que tous les corps tombent de la même façon dans un champ de gravitation, quelles que soient leur masse ou leur composition chimique. Cette observation, a priori fortuite, en théorie newtonienne, et remarquablement vérifiée expérimentalement, est formalisée sous le nom de principe d'équivalence et amène naturellement à considérer que la gravitation est une manifestation de la géométrie de l'espace-temps.

La théorie ainsi construite, qui porte le nom de relativité générale, incorpore le principe de relativité, et la théorie newtonienne en est une approximation dans la limite des champs gravitationnels faibles et des vitesses petites devant celle de la lumière. En effet, les déformations de l'espace-temps prévues sous l'effet des corps massifs, quand ceux-ci ont une forte accélération, ne se propagent pas plus vite que la vitesse de la lumière, ce qui résout le paradoxe de l'instantanéité apparente de l'interaction newtonienne. Il en résulterait des ondes gravitationnelles, qui restent encore à observer.

Gravitation et astronomie[modifier | modifier le code]

Article général Pour un article plus général, voir astronomie.

La gravitation newtonienne est suffisante pour décrire la majorité des phénomènes observés à l'échelle des étoiles. Elle suffit, par exemple, pour décrire l'évolution des planètes du Système solaire, à quelques détails près comme l'avance du périhélie de Mercure et l'effet Shapiro.

Mais la relativité générale est nécessaire pour modéliser certains objets et phénomènes astronomiques particuliers : les étoiles à neutrons, les mirages gravitationnels, les objets très compacts tels que les trous noirs, etc.

Gravitation et cosmologie[modifier | modifier le code]

Effet de mirage gravitationnel prédit par la relativité générale. Les forts champs gravitationnels déforment l'espace autour d'eux ce qui courbe la trajectoire empruntée par les rayons lumineux, déformant ainsi certaines images que nous recevons du cosmos.
Article général Pour un article plus général, voir cosmologie.

La gravitation étant la force dominante à l'échelle des distances astronomiques, les théories newtonienne et einsteinienne ont été confrontées depuis leurs créations respectives aux observations de la structure à grande échelle de l'univers. Si aux échelles des étoiles et des galaxies, la gravitation newtonienne est suffisante, dans beaucoup de situations, la théorie newtonienne est en difficulté. Par exemple, elle est incapable d'offrir une description cohérente d'un univers homogène infini. En revanche, la relativité générale est parfaitement en mesure de décrire une telle situation.

La relativité générale seule ne suffit cependant pas pour décrire la structure à grande échelle de l'univers. Il faut lui adjoindre des hypothèses sur la répartition spatiale de la matière. Les observations indiquent qu'à grande échelle, l'univers est remarquablement homogène (à plus petite échelle, la matière est bien sûr répartie de façon non uniforme : l'espace entre les étoiles d'une même galaxie est essentiellement vide, tout comme l'espace entre les galaxies). Ce fait observationnel avait au départ été supposé par Einstein, qui lui avait donné le nom de principe cosmologique. Sous cette hypothèse, la relativité générale permet, assez facilement du reste, une modélisation cohérente de l'univers. Il existe cependant, outre la matière visible constituant les étoiles, et le gaz des galaxies, une matière noire aux propriétés et à la distribution encore très mal connues.

La dynamique de l'univers va, elle, dépendre des propriétés de la matière qui le compose, en particulier de son équation d'état. On peut montrer que, sauf cas particulier, l'univers ne peut être statique : il est soit en contraction, soit en expansion globales. De toute manière, une structure globale uniforme de l'univers serait instable : les parties les plus denses, même très faiblement, finiraient par s'effondrer sous leur propre poids, attirant la matière des parties les moins denses, et les laissant entièrement vides. (Cependant, à moyenne échelle, l'Univers a une "structure d'éponge" et il existe d'énormes bulles sans matière visible).

Bien que la théorie de "l'Expansion" tienne peu compte des nombreuses interactions existant entre la matière et les rayonnements électromagnétiques (sinon, par exemple, seul le radar existerait ; on n'aurait pas de four à micro-ondes) ; les observations confirment globalement cette prédiction puisque l'on observe une récession apparente des galaxies, celles-ci s'éloignant de nous d'autant plus vite qu'elles sont éloignées. Le décalage spectral des lumières lointaines fut découvert par Edwin Hubble à la fin des années 1920. Plus tard, son élève, Allan Sandage introduisit le concept de l'Expansion, suite aux travaux de Lemaître et Gamow. Elle indique que l'univers tel que nous le connaissons est issu d'une phase extraordinairement dense et chaude : le Big Bang. Plusieurs observations quantitatives confirment l'histoire du Big Bang, à partir de sa première minute. Le destin de l'univers n'est pas connu avec certitude, car le comportement à long terme de la matière est incertain. On a observé une accélération de l'expansion de l'univers, due à une force de répulsion à très longue distance, prévue comme une possibilité dans la Relativité Générale. Ceci semble être le signe probable que l'expansion durera indéfiniment, sans donner lieu à une phase de recontraction (Big Crunch) ou ; que cette expansion n'est qu'une apparence, très commode pour rendre compte de nombreuses observations.

Gravitation et physique quantique[modifier | modifier le code]

Article général Pour un article plus général, voir physique quantique.

La relativité générale a été conçue sur l'hypothèse de la continuité de l'espace-temps (et même sa différentiabilité) et sur l'hypothèse de la continuité de la matière (entre autres pour construire le tenseur de densité d'énergie-impulsion). Cette deuxième hypothèse est clairement une approximation au regard de la physique quantique.

La physique quantique étant l'exploration de l'infiniment petit, l'expérimentation de la gravitation dans ce cadre se heurte à un problème majeur : les trois autres forces qui y règnent sont au moins 1025 fois plus fortes, alors qu'il est déjà difficile d'expérimenter sur elles ; du coup les effets de la gravitation se perdent dans les inévitables imprécisions des mesures.

Cette difficulté expérimentale n'a pas empêché les tentatives théoriques de construire une gravitation quantique, sans résultat susceptible à ce jour de vérification expérimentale.

On peut toutefois remarquer que :

  1. L'ajout du potentiel gravitationnel à l'équation de Schrödinger permet de retrouver un résultat connu : les particules tombent.
  2. L'utilisation des intégrales de chemin de Feynman a permis de prévoir un déphasage de la fonction d'onde dû à la gravitation (galiléenne) ; ces deux effets correspondent à une approximation semi-classique en mécanique quantique.
  3. L'équation des ondes gravitationnelles peut s'interpréter comme celle de la propagation d'une particule appelée graviton, jugée responsable de la gravitation, dont on peut déduire certaines propriétés (notamment sa masse, nulle, et son spin, égal à 2), sans que cela ait pu encore être vérifié expérimentalement malgré les tentatives de plus en plus sophistiquées.

Exemples de théories quantiques de la gravitation : Théorie M, Supergravité, géométrie non commutative, gravitation quantique à boucles.

Notes et références[modifier | modifier le code]

  1. ↑ À condition de ne pas comparer la chute d'une bille et celle d'une feuille d'automne.
  2. ↑ La valeur précise est variable suivant le lieu sur terre.
  3. ↑ L’incertitude relative sur cette constante est cependant élevée par rapport à d’autres constantes fondamentales : 1 pour 10 000, soit une incertitude absolue de ± 0,000 67×10-11 N⋅m2⋅kg-2. cf. CODATA 2006 sur le site du NIST [archive].


Voir aussi[modifier | modifier le code]

Sur les autres projets Wikimedia :

Articles connexes[modifier | modifier le code]

Bibliographie[modifier | modifier le code]



28/10/2013
0 Poster un commentaire

A découvrir aussi


⨯

Inscrivez-vous au blog

Soyez prévenu par email des prochaines mises à jour

Rejoignez les 525 autres membres