En poursuivant votre navigation sur ce site, vous acceptez l'utilisation de cookies pour vous proposer des services et offres adaptés à vos centres d'intéréts.

Constante d'Einstein

Constante d'Einstein

Un article de Wikipédia, l'encyclopédie libre.

En 1916, Albert Einstein propose de décrire l'univers à l'aide d'une équation de champ, tensorielle. Celle-ci contient deux constantes, qui n'ont strictement rien à voir l'une avec l'autre. La première est la constante d'Einstein, figurée dans le second membre par la lettre \scriptstyle C majuscule ou (const) dans la première équation écrite ci-dessous. La seconde est la constante cosmologique \scriptstyle\Lambda.

On se propose dans ce qui va suivre de déterminer la valeur de la constante d'Einstein. Pour ce faire on partira d'une équation de champ à constante cosmologique nulle et d'une hypothèse de stationnarité. Puis on passera à l'approximation newtonienne en introduisant les hypothèses : champ faible et vitesses faibles devant celle de la lumière.

On verra alors apparaître la loi de Newton et son corollaire l'équation de Poisson.

En quelque sorte, dans cette approximation, l'équation de Poisson apparaît comme la forme approchée de l'équation de champ (ou l'équation de champ se présente comme une généralisation de l'équation de Poisson). L'identification permet d'obtenir l'expression de la constante d'Einstein en fonction des grandeur 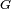\scriptstyle G (constante gravitationnelle) et \scriptstyle c (vitesse de la lumière).

Sommaire

[masquer]

L’équation de champ dans un espace non-vide [modifier]

Nous devons obtenir un tenseur susceptible de décrire la géométrie de l’espace en présence d’un champ d’énergie. Cette équation a été proposée par Einstein en 1917 et s’écrit :

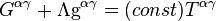
G^{\alpha\gamma} + \Lambda \mathrm{g}^{\alpha\gamma} = (const) T^{\alpha\gamma}~

\scriptstyle\Lambda est ce qu’on appelle la constante cosmologique. Nous allons nous placer dans une situation où celle-ci est prise égale à zéro. L’équation de champ devient alors :

G^{\alpha\gamma} = \left( R^{\alpha\gamma} - \frac{1}{2} \mathrm{g}^{\alpha\gamma} R \right) = CT^{\alpha\gamma}~

où \scriptstyle C est une constante. Nous allons déterminer sa valeur dans la section suivante.

Au prix d’une certaine manipulation nous allons écrire cette équation sous une autre forme. Contractons les indices dans l'équation ci-dessus :

{R^\alpha}_\alpha - \frac{1}{2}{\mathrm{g}^\alpha}_\alpha R = {CT^\alpha}_\alpha~

Ainsi :

R = -{CT^\alpha}_\alpha = -CT~

En utilisant ce résultat nous pouvons écrire l’équation de champ sous la forme :

R^{\alpha\gamma} = C \left(T^{\alpha\gamma} - \frac{1}{2} \mathrm{g}^{\alpha\gamma} T \right)~

La limite classique des équations de la gravitation [modifier]

Nous souhaitons que cette équation de champ d'Einstein soit une généralisation de l’équation de Poisson :

\sum_{i=1}^3 \varphi_{|i|i}=\frac{\partial {}^2 \varphi}{(\partial {x^1})^2} + \frac{\partial {}^2 \varphi}{(\partial {x^2})^2} + \frac{\partial {}^2 \varphi}{(\partial {x^3})^2}=4\pi G \rho

Rappelons un peu les notations utilisées. Un point-événement est décrit par les quatre coordonnées :

\displaystyle x^0, x^1, x^2, x^3

La première est la coordonnée de temps et les trois autres les coordonnées d’espace.

Les écritures |i\, et |i|j\, désignent respectivement \frac{\partial}{\partial x^i} et \frac{\partial^2}{\partial x^i \partial x^j}.

Ainsi : |i|i\, signifie \frac{\partial^2}{(\partial {x^i})^2}.

Nous allons considérer un champ de matière où celle-ci a une densité ρ faible et se déplace à une vitesse également faible. Le tenseur-matière relativiste est :

T^{\mu\nu}= \rho \begin{pmatrix} 1 & \nu_x / c & \nu_y / c & \nu_z / c\\ \nu_x / c & \nu^2_x / c^2 & \nu_x \nu_y / c^2 & \nu_x \nu_z / c^2\\ \nu_y / c & \nu_y \nu_x / c^2 & \nu^2_y / c^2 & \nu_y \nu_z / c^2\\ \nu_z / c & \nu_z \nu_x / c^2 & \nu_z \nu_y / c^2 & \nu^2_z / c^2 \end{pmatrix}

Si on néglige les termes de l’ordre de \left(\frac{\nu}{c}\right)^2 et \rho \left(\frac{\nu}{c}\right) il prend la forme :

T^{\mu\nu}= \begin{pmatrix} \rho_0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{pmatrix}

On va ensuite supposer que l’écoulement soit stationnaire et donc fonder notre géométrie sur une métrique indépendante du temps. Utilisant les coordonnées de la relativité Restreinte ct,x,y,z qu’on écrira ici :

\displaystyle x^0, x^1, x^2, x^3

Appliquant une méthode de perturbations, nous allons considérer une métrique qui se présente sous la forme d’une somme de deux termes. Le premier est la métrique de Lorentz,

\displaystyle \eta_{\mu\nu}

qui est celle de l'espace de Minkowski, sans courbure. Si on explicite on obtient :

\displaystyle \mathrm{d}s^2 = (\mathrm{d}x^0)^2 - (\mathrm{d}x^1)^2 - (\mathrm{d}x^2)^2 - (\mathrm{d}x^3)^2

Le second terme correspond à la perturbation et est également indépendant du temps :

\displaystyle \varepsilon\gamma_{\mu\nu}

Ainsi nous écrirons notre métrique

\displaystyle g_{\mu\nu} = \eta_{\mu\nu} + \varepsilon\gamma_{\mu\nu}

En explicitant l’élément de longueur :

\displaystyle \mathrm{d}s^2 = (\mathrm{d}x^0)^2 - (\mathrm{d}x^1)^2 - (\mathrm{d}x^2)^2 - (\mathrm{d}x^3)^2 + \varepsilon\gamma_{\mu\nu}\mathrm{d}x^{\mu}\mathrm{d}x^{\nu}

Si nous négligeons les termes de l’ordre de

\displaystyle \varepsilon\rho_0

Le scalaire de Laue

\displaystyle T^{\mu}_{\mu}

devient :

T^{\mu}_{\mu} = Tr = \begin{pmatrix} \rho_0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{pmatrix} = \rho_0

et le second membre de l’équation, au premier ordre par rapport aux quantités \textstyle \rho_0, \textstyle \frac{\nu}{c} et \textstyle \varepsilon\gamma_{\mu\nu} s’écrit :

\begin{align}C\left(T_{\mu\nu}-\frac{1}{2} g_{\mu\nu}T \right)&\simeq C\left(T_{\mu\nu}-\frac{1}{2} g_{\mu\nu} T \right) \\ & \simeq C \left[ \begin{pmatrix} \rho_0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{pmatrix} - \frac{1}{2}\begin{pmatrix} \rho_0 & 0 & 0 & 0\\ 0 & -\rho_0 & 0 & 0\\ 0 & 0 & -\rho_0 & 0\\ 0 & 0 & 0 & -\rho_0 \end{pmatrix} \right] \\ & \simeq \frac{C\rho_0}{2} \delta_{\mu\nu} \end{align}

En négligeant les termes du second ordre dans le terme de perturbation de la métrique nous pouvons écrire une forme approchée du tenseur de Riemann contracté :

R_{\mu\nu} \cong \frac{1}{2}\left[\ln(-g)\right]_{|\mu|\nu|}- \begin{Bmatrix} & \beta & \\ \\ \mu & & \nu \end{Bmatrix}_{|\beta}

Ainsi la forme approchée des équations de champ devient :

\frac{1}{2}\left[\ln(-g)\right]_{|\mu|\nu|}- \begin{Bmatrix} & \beta & \\ \\ \mu & & \nu \end{Bmatrix}_{|\beta} = \frac{C\rho_0}{2} \delta_{\mu\nu}

Considérons d’abord le cas μ = ν = 0. Comme nous avons pris une métrique indépendante du temps, le premier terme de l'équation ci-dessus est nul. Il nous reste l’équation :

\begin{Bmatrix} & \beta & \\ \\ 0 & & 0 \end{Bmatrix}_{|\beta} = \left(g^{\alpha\beta}\left[00,\alpha\right]\right)_{|\beta} = -\frac{C\rho_0}{2}\qquad\qquad (*)

Les symboles de Christoffel du premier genre sont définis par :

\left[00,\alpha\right] = \frac{1}{2}\left(g_{0\alpha|0} + g_{\alpha 0|0} - g_{00|\alpha}\right)

Comme la métrique de Lorentz est constante dans l’espace et dans le temps ceci se simplifie en :

\left[00,\alpha\right] = -\frac{\varepsilon}{2} \gamma_{00|\alpha}

De plus comme le terme de perturbation dans la métrique est également indépendant du temps ceci entraîne que l'élément \left[00,0\right] est nul. En négligeant les termes du second ordre dans le terme de perturbation nous obtenons :

g^{\beta\alpha} \left[00,\alpha\right] = \frac{\varepsilon}{2} \gamma_{00|\beta}

qui est nul si β = 0 (ce qui correspond alors à la dérivée par rapport au temps). En substituant dans 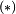\scriptstyle (*) nous obtenons l’équation :

\varepsilon\sum_{\beta = 0}^{3} \gamma_{00|\beta|\beta} = -C\rho_0

Laquelle, du fait que la métrique est indépendante du temps peut tout simplement s’écrire :

\varepsilon\sum_{\beta = 1}^{3} \gamma_{00|\beta|\beta} = -C\rho_0

Rappelons ce que signifie cette notation. C’est une simple convention d’écriture. Cette équation peut s'écrire :

\sum_{\beta = 0}^{3} \gamma_{00|\beta|\beta} = \sum_{i=1}^3 \frac{\partial {}^2 \gamma_{00}}{\partial {x_{\beta}}^2} = \frac{\partial {}^2 \gamma_{00}}{\partial {x_1}^2} + \frac{\partial {}^2 \gamma_{00}}{\partial {x_2}^2} + \frac{\partial {}^2 \gamma_{00}}{\partial {x_3}^2} = -C\rho_0

qui peut être identifiée à l’équation de Poisson si nous écrivons :

-\frac{\varepsilon\gamma_{00}}{C} = \frac{\varphi}{4\pi G}

On montre ainsi que la théorie classique (équation de Poisson) se présente comme le cas limite (champ faible, vitesses faibles devant la vitesse de la lumière) d’une théorie relativiste où la métrique ne dépend pas du temps.

Pour être complet il faut montrer que la gravité peut être assimilée à un phénomène métrique. Sans détailler tous les intermédiaires de calcul nous ne donnerons que la description schématique de ce calcul dont l'étudiant pourra trouver le détail dans tous les ouvrages consacrés à l'enseignement de la relativité Générale. On part encore d’une métrique de Lorentz perturbée qu’on écrira :

\displaystyle g_{\mu\nu} = \eta_{\mu\nu} + \varepsilon\gamma_{\mu\nu}

explicitée :

\displaystyle \mathrm{d}s^2 = (\mathrm{d}x^0)^2 - (\mathrm{d}x^1)^2 - (\mathrm{d}x^2)^2 - (\mathrm{d}x^3)^2 + \varepsilon\gamma_{\mu\nu}\mathrm{d}x^{\mu}\mathrm{d}x^{\nu}

On supposera que la vitesse \scriptstyle \nu est faible devant la vitesse de la lumière \scriptstyle c en faisant apparaître un petit paramètre \scriptstyle \beta \textstyle = \frac{\nu}{c}.

On a :

\displaystyle x^0 = ct

On peut écrire :

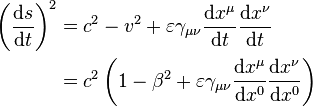
\begin{align} \left(\frac{\mathrm{d}s}{\mathrm{d}t}\right)^2 &= c^2 - v^2 + \varepsilon\gamma_{\mu\nu} \frac{\mathrm{d}x^{\mu}}{\mathrm{d}t} \frac{\mathrm{d}x^{\nu}}{\mathrm{d}t}\\ &= c^2 \left(1 - \beta^2 + \varepsilon\gamma_{\mu\nu} \frac{\mathrm{d}x^{\mu}}{\mathrm{d}x^0} \frac{\mathrm{d}x^{\nu}}{\mathrm{d}x^0}\right) \end{align}

En se limitant au premier ordre en \scriptstyle\beta et \scriptstyle\varepsilon on obtient :

\left(\frac{\mathrm{d}s}{\mathrm{d}t}\right)^2 \cong c^2(1 + \varepsilon\gamma_{00})

On écrit ensuite le système d’équations différentielles donnant les géodésiques, que l'étudiant trouvera dans tous les ouvrages classiques. On calcule les symboles de Christoffel. L’équation donnant les géodésiques devient :

\frac{\mathrm{d}^2 x^{\alpha}}{\mathrm{d}t^2} + \begin{Bmatrix} & \alpha & \\ \\ 0 & & 0 \end{Bmatrix} c^2 = 0 \qquad (**)

La forme approchée du symbole de Christoffel se trouve être :

\begin{Bmatrix} & i & \\ \\ 0 & & 0 \end{Bmatrix} = \frac{1}{2}\varepsilon\gamma_{00|i}

En introduisant ce résultat dans l’équation des géodésiques \scriptstyle (**) on obtient :

\displaystyle \frac{\mathrm{d}^2 x^i}{\mathrm{d}t^2} = -\frac{c^2}{2} \varepsilon \gamma_{00|i}

C’est une équation vectorielle. Comme on a fait l’hypothèse que la métrique était indépendante du temps ceci ne concerne que les variables d’espace. Donc le second membre de l’équation est un gradient.

En codant le vecteur-position par la lettre \scriptstyle X et le gradient par le vecteur \scriptstyle \nabla nous pouvons écrire ceci :

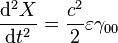
\displaystyle \frac{\mathrm{d}^2 X}{\mathrm{d}t^2} = \frac{c^2}{2} \varepsilon \gamma_{00}

Ceci n’est rien d’autre que la loi de Newton de la théorie classique, dérivant du potentiel gravitationnel \scriptstyle\varphi, si nous faisons l’identification :

\varphi = -\frac{c^2}{2} \varepsilon \nabla \gamma_{00}

Inversement, si on se donne un potentiel gravitationnel \scriptstyle\varphi, le mouvement d’une particule s’inscrira selon une géodésique de l’espace-temps si le premier terme du tenseur métrique a la forme :

g_{00} = 1 + \frac{2\varphi}{c^2}

Cette étape est importante. La loi de Newton apparaît donc comme un des aspects de la Relativité Générale dans la double approximation :

  • champ gravitationnel faible
  • vitesses faibles devant c

Reprenons notre raisonnement depuis le début.

  • Nous avons considéré une métrique g qui soit solution de l’équation d’Einstein (avec une constante cosmologique Λ nulle).
  • Nous avons supposé que cette métrique représentait une faible perturbation vis à vis d’une métrique de Lorentz η (espace relativiste stationnaire et plat),
  • Nous avons supposé que ce terme de perturbation ne dépendait pas du temps. Comme la métrique de Lorentz n’en dépend pas non plus, cette métrique g est aussi indépendante du temps.
  • Nous avons effectué des développements en série de manière à obtenir une linéarisation de l’équation de champ d’Einstein.
  • Nous avons trouvé que cette forme linéarisée pouvait être identifiée à l’équation de Poisson en faisant recours à un travail annexe où on montre que « champ de gravitation égale courbure », en liant le terme de perturbation de la métrique au potentiel gravitationnel selon la relation :
\varphi = \frac{c^2}{2} \varepsilon \gamma_{00}

En prime, ceci nous fournit la valeur de la constante C, dite « constante d’Einstein » (qui n’a rien à voir avec la « constante cosmologique Λ » ).

C= -\frac{8\pi G}{c^2}

Nous pouvons alors écrire l'équation de champ :

G^{\alpha\gamma} + \Lambda g^{\alpha\gamma} = -\frac{8\pi G}{c^2} T^{\alpha\gamma}

Remarque 1 [modifier]

Certains lecteurs verront dans ce résultat une différence avec la valeur indiquée dans d'autres pages de Wikipedia, par exemple celle consacrée à la constante cosmologique, qui figure également dans le portail cosmologie et qui est :

C=-\frac{8\pi G}{c^4}

Il ne s'agit d'une erreur ni chez les uns, ni chez les autres. Tout dépend de la façon dont on décide d'écrire le tenseur impulsion-énergie. Si on considère la vitesse de la lumière c comme une constante absolue alors ces deux présentations sont strictement équivalentes. Si dans ce calcul on avait écrit le tenseur impulsion-énergie sous la forme :

T^{\mu\nu}= \rho \begin{pmatrix} c^2 & \nu_x c & \nu_y c & \nu_z c\\ \nu_x c & \nu^2_x & \nu_x \nu_y & \nu_x \nu_z\\ \nu_y c & \nu_y \nu_x & \nu^2_y & \nu_y \nu_z\\ \nu_z c & \nu_z \nu_x & \nu_z \nu_y & \nu^2_z \end{pmatrix}

et la trace correspondante :

T^\mu_\mu=Tr \begin{pmatrix} \rho_0 c^2 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{pmatrix}=\rho_0 c^2

alors on aurait obtenu la valeur de la constante d'Einstein :

C=-\frac{8\pi G}{c^4}

et l'équation de champ s'écrirait :

G^{\alpha\gamma}+\Lambda g^{\alpha\gamma}=-\frac{8\pi G}{c^4}T^{\alpha\gamma}

Récemment (postérieurement à 2005) par exemple, Monique Signore, directeur de recherche associé à l'Observatoire de Paris, a publié un article intitulé "Principes de base de la relativité générale" où elle utilise la lettre Grecque χχpour désigner la constante d'Einstein, où elle fait figurer la vitesse de la lumière par son carré.

Remarque 2 [modifier]

L’équation d’Einstein est « à divergence nulle ». La divergence nulle du tenseur énergie-impulsion (energy-momentum tensor) est l’expression géométrique de la loi de conservation. Cette contrainte implique que la constante d’Einstein soit une constante absolue, sinon il y aurait violation de ce postulat.

Mais, comme cette constante d’Einstein a été évaluée en fondant le calcul sur une métrique indépendante du temps ceci n’implique nullement la constance absolue de G et de c mais seulement la constance absolue du rapport :

\frac{G}{c^2}

Références [modifier]

  • (en) Introduction to General Relativity (Ronald Adler, Maurice Bazin, Menahem Schiffer), Mcgraw-Hill, June 1975 - ISBN 0070004234
Portail de la physique
Portail de la cosmologie
Récupérée de « http://fr.wikipedia.org/wiki/Constante_d%27Einstein »


16/09/2007
0 Poster un commentaire

A découvrir aussi


⨯

Inscrivez-vous au blog

Soyez prévenu par email des prochaines mises à jour

Rejoignez les 525 autres membres