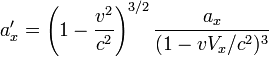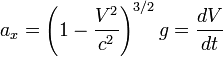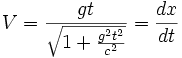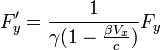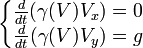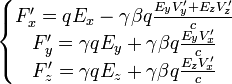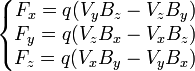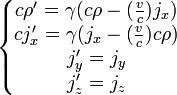Calculs relativistes - Partie 2
Forces et Accélérations [modifier]
Le quadrivecteur accélération [modifier]
De même que nous avons défini le quadrivecteur vitesse en différentiant le quadrivecteur position par rapport au temps propre, nous pouvons définir le quadri-accélération en différentiant le quadrivecteur vitesse par rapport au temps propre :
avec 
La transformation des accélérations [modifier]
La transformation de Lorentz appliquée sur le quadrivecteur accélération dans un référentiel  permet d'en déduire le quadrivecteur accélération dans le référentiel
permet d'en déduire le quadrivecteur accélération dans le référentiel  , et de calculer explicitement les composantes de l'accélération. Notons
, et de calculer explicitement les composantes de l'accélération. Notons  la ième composante dans le référentiel
la ième composante dans le référentiel  et notons-la
et notons-la  dans le repère
dans le repère  . On obtient, en notant v la vitesse de
. On obtient, en notant v la vitesse de  par rapport à
par rapport à  :
:
Le mouvement uniformément accéléré [modifier]
Considérons un référentiel inertiel  . Supposons que M, particule de masse m0, se déplace sous l'effet d'une force constante F parallèle à Ox et que, pour t = 0, M soit en O avec une vitesse nulle. Sous l'effet de la force, la particule va être soumise à une accélération. Cependant, celle-ci ne saurait être constante, égale à
. Supposons que M, particule de masse m0, se déplace sous l'effet d'une force constante F parallèle à Ox et que, pour t = 0, M soit en O avec une vitesse nulle. Sous l'effet de la force, la particule va être soumise à une accélération. Cependant, celle-ci ne saurait être constante, égale à 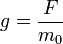 , sous peine de voir la particule atteindre puis dépasser la vitesse de la lumière. Quel est alors l'équivalent relativiste du mouvement uniformément accéléré de la mécanique galiléenne ?
, sous peine de voir la particule atteindre puis dépasser la vitesse de la lumière. Quel est alors l'équivalent relativiste du mouvement uniformément accéléré de la mécanique galiléenne ?
À un instant t donné, le point M est animé d'une vitesse V par rapport à  . Considérons alors un référentiel
. Considérons alors un référentiel  se déplaçant à la vitesse constante v qui coïncide à l'instant t avec la vitesse V de M, et tel que son origine O' coïncide également avec M à l'instant t. Dans ce référentiel
se déplaçant à la vitesse constante v qui coïncide à l'instant t avec la vitesse V de M, et tel que son origine O' coïncide également avec M à l'instant t. Dans ce référentiel  , au cours du temps, le point M se voit se rapprocher de O', atteindre ce point en un certain instant t', sa vitesse V' s'annule en cet instant, puis il repart et s'éloigne de O'. Il est alors soumis à une accélération a'x dans le repère
, au cours du temps, le point M se voit se rapprocher de O', atteindre ce point en un certain instant t', sa vitesse V' s'annule en cet instant, puis il repart et s'éloigne de O'. Il est alors soumis à une accélération a'x dans le repère  . Puisque la vitesse V' s'annule au moment où M atteint O', nous ferons l'hypothèse que les lois de la mécanique galiléenne s'applique à cet instant, et que l'accélération a'x est égale à g. Selon les règles de transformation des accélérations vues précédemment, et compte tenu du fait que v = V = Vx, l'accélération de la particule M dans le référentiel
. Puisque la vitesse V' s'annule au moment où M atteint O', nous ferons l'hypothèse que les lois de la mécanique galiléenne s'applique à cet instant, et que l'accélération a'x est égale à g. Selon les règles de transformation des accélérations vues précédemment, et compte tenu du fait que v = V = Vx, l'accélération de la particule M dans le référentiel  à l'instant t est
à l'instant t est  .
.
Si, à chaque instant t, on redéfinit le référentiel  coïncidant avec M, alors on définit ainsi une accélération propre constante a'x = g et une accélération dans le référentiel
coïncidant avec M, alors on définit ainsi une accélération propre constante a'x = g et une accélération dans le référentiel  égale à :
égale à :
Au fur et à mesure que V augmente et se rapproche de c, l'accélération de la particule dans le référentiel  diminue, bien que son accélération dans son référentiel propre reste constante. L'intégration de l'équation donne l'expression de V en fonction du temps, à savoir :
diminue, bien que son accélération dans son référentiel propre reste constante. L'intégration de l'équation donne l'expression de V en fonction du temps, à savoir :
On constate que V tend vers c lorsque t tend vers l'infini. Par ailleurs, pour t proche de 0, on retrouve l'expression V = gt de la mécanique galiléenne. Une deuxième intégration fournit l'expression de l'abscisse x du point mobile M :
Pour t proche de 0, on retrouve l'expression 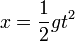 de la mécanique galiléenne.
de la mécanique galiléenne.
Accélération et énergie [modifier]
Si, dans l'étude du paragraphe précédent, on souhaite que la loi 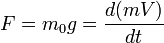 reste valide, il faut, puisque dV/dt n'est pas constant, que m ne le soit pas non plus. F étant constante, on a nécessairement mV = Ft avec, comme on l'a vu :
reste valide, il faut, puisque dV/dt n'est pas constant, que m ne le soit pas non plus. F étant constante, on a nécessairement mV = Ft avec, comme on l'a vu :
ce qui donne :
On obtient alors :
Ainsi, lorsque V augmente, on est amené à attribuer une masse m en mouvement de plus en plus importante, afin que la loi fondamentale de la dynamique reste valide.
E = mc2 [modifier]
Toujours dans le cadre de l'étude précédente, la particule M voit son énergie varier avec la puissance suivante :
or :
-
 et
et 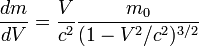
d'où, après simplification :
ce qui conduit à la formule la plus célèbre de la physique :

On remarque que la variation d'énergie depuis l'instant initial est :
qui donne  pour les petites vitesses. On retrouve l'expression classique de l'énergie cinétique.
pour les petites vitesses. On retrouve l'expression classique de l'énergie cinétique.
Le quadrivecteur force et la transformation des forces [modifier]
Soit une particule de masse m0, se déplaçant à la vitesse 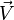 par rapport à un référentiel inertiel
par rapport à un référentiel inertiel  . On peut, comme en mécanique classique, définir la force à laquelle est soumise cette particule si sa quantité de mouvement varie, par :
. On peut, comme en mécanique classique, définir la force à laquelle est soumise cette particule si sa quantité de mouvement varie, par :
avec  , et sa variation d'énergie par :
, et sa variation d'énergie par :
Mais pour passer d'un référentiel à l'autre, il vaut mieux utiliser le quadrivecteur force défini comme la dérivée du quadrivecteur impulsion par rapport au temps propre :
L'application d'une transformation de Lorentz à ce quadrivecteur permet de savoir comment une force se transforme d'un référentiel à l'autre.
Si (Fx,Fy,Fz) sont les composantes de 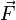 dans le référentiel
dans le référentiel  et si (F'x,F'y,F'z) sont ses composantes dans le référentiel
et si (F'x,F'y,F'z) sont ses composantes dans le référentiel  en translation de vitesse v par rapport à
en translation de vitesse v par rapport à  , alors on trouve que :
, alors on trouve que :
avec  et
et 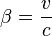 .
.
En particulier, si la vitesse V du point mobile coïncide à un instant donné avec la vitesse v du référentiel  , alors F'x = Fx, par contre les deux autres composantes sont différentes.
, alors F'x = Fx, par contre les deux autres composantes sont différentes.
Exemple 1 : chute libre [modifier]
Considérons une particule de masse m0 située en t = 0 en O et se déplaçant à la vitesse v selon l'axe Ox. On lui applique une force constante F = m0g selon l'axe Oy. En mécanique galiléenne, sa trajectoire est une parabole. Qu'en est-il en mécanique relativiste ?
En écrivant que 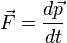 et en projetant cette relation sur deux axes, on obtient, en notant Vx et Vy les composantes de sa vitesse V à l'instant t :
et en projetant cette relation sur deux axes, on obtient, en notant Vx et Vy les composantes de sa vitesse V à l'instant t :
d'où :
La résolution de ce système conduit à :
et l'intégration de ces deux relations donnent les coordonnées x et y de la particule à l'instant t :
où sinh-1 est la réciproque du sinus hyperbolique. Si on exprime y en fonction de x, on obtient :
qui est l'équation d'une chaînette et non plus d'une parabole.
On peut retrouver les solutions de la mécanique galiléenne en augmentant indéfiniment la valeur de c, ce qui donne :
Exemple 2 : champ électrique [modifier]
On considère dans le référentiel  un champ électrique
un champ électrique  , et une particule de charge q, se déplaçant dans ce champ. Celle-ci est soumise à une force
, et une particule de charge q, se déplaçant dans ce champ. Celle-ci est soumise à une force  . Qu'en est-il dans le référentiel
. Qu'en est-il dans le référentiel  en déplacement à la vitesse v parallèle à Ox par rapport à
en déplacement à la vitesse v parallèle à Ox par rapport à  ?
?
À partir des relations :
avec 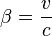 et
et  , on en déduit que :
, on en déduit que :
La force  est de la forme :
est de la forme :
avec 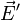 champ électrique de composantes
champ électrique de composantes  et
et  champ magnétique de composantes
champ magnétique de composantes 
Ainsi, le fait de changer de référentiel a légèrement modifié les composantes du champ électrique orthogonales au déplacement, et a fait apparaître un champ magnétique. Ce champ n'est que l'effet relativiste du changement de référentiel.
On notera que 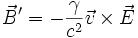
Exemple 3 : champ magnétique [modifier]
On considère maintenant la même particule, mais dans un champ magnétique 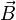 . La force à laquelle la particule est soumise est cette fois :
. La force à laquelle la particule est soumise est cette fois :
Les composantes de cette force sont :
En opérant comme dans le paragraphe précédent, on trouve les composantes de la force dans le référentiel  :
:
La force  est de la forme :
est de la forme :
avec ici 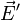 champ électrique de composantes
champ électrique de composantes  et
et  champ magnétique de composantes
champ magnétique de composantes  .
.
Ainsi, le fait de changer de référentiel a légèrement modifié les composantes du champ magnétique orthogonales au déplacement, et a fait apparaître un champ électrique. Ce champ est là aussi un effet relativiste du changement de référentiel.
On notera que 
Si on combine les exemples 2 et 3, on obtient les transformations d'un champ électro-magnétique  :
:
ou encore, en désignant par  et
et 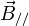 les composantes des champs parallèles au sens du déplacement du référentiel
les composantes des champs parallèles au sens du déplacement du référentiel  , et par
, et par  et
et  les composantes orthogonales :
les composantes orthogonales :
Tout ceci fait intervenir deux champs  classiques qui lors d'un changement de référentiel se 'transforment' l'un dans l'autre sans pour cela se mettre clairement sous la forme de quadrivecteur comme l'énergie impulsion etc. Par contre les équations de Maxwell prennent une forme relativiste et
classiques qui lors d'un changement de référentiel se 'transforment' l'un dans l'autre sans pour cela se mettre clairement sous la forme de quadrivecteur comme l'énergie impulsion etc. Par contre les équations de Maxwell prennent une forme relativiste et 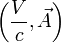 va se transformer comme doit le faire un quadrivecteur ce qui fait dire à Feynman que si dans les champs électromagnétique il fallait mettre une hiérarchie c'est de considérer d'abord les grandeurs quadrivecteurs. Il faut donc essayer de formuler les équations de Maxwell avec des opérateurs et des champs vectoriels ou tensoriel à 4 dimensions.
va se transformer comme doit le faire un quadrivecteur ce qui fait dire à Feynman que si dans les champs électromagnétique il fallait mettre une hiérarchie c'est de considérer d'abord les grandeurs quadrivecteurs. Il faut donc essayer de formuler les équations de Maxwell avec des opérateurs et des champs vectoriels ou tensoriel à 4 dimensions.
Optique relativiste [modifier]
On utilise en optique relativiste les quadrivecteurs de la forme  , où ω est la pulsation de l'onde, et
, où ω est la pulsation de l'onde, et 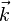 le vecteur d'onde indiquant la direction de propagation de l'onde et de module ω/c. Ce quadrivecteur est l'équivalent pour une onde électromagnétique du quadrivecteur
le vecteur d'onde indiquant la direction de propagation de l'onde et de module ω/c. Ce quadrivecteur est l'équivalent pour une onde électromagnétique du quadrivecteur  énergie-impulsion pour une particule, multiplié par la constante de Planck
énergie-impulsion pour une particule, multiplié par la constante de Planck  . En effet, la dualité onde-particule attribue à une onde une énergie
. En effet, la dualité onde-particule attribue à une onde une énergie 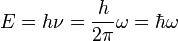 , et une quantité de mouvement dont le module est
, et une quantité de mouvement dont le module est  .
.
La transformation d'un référentiel à l'autre de ce quadrivecteur explique les deux effets suivants :
Le quadrivecteur énergie impulsion [modifier]
Pour exprimer le quadrivecteur énergie impulsion d'une particule de masse m0 se déplaçant à la vitesse 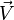 , il suffit de considérer une masse m0 et de former comme en mécanique classique l'impulsion qui est le produit de la masse par la vitesse.
, il suffit de considérer une masse m0 et de former comme en mécanique classique l'impulsion qui est le produit de la masse par la vitesse.
En mécanique relativiste, nous formons le produit de la masse par la quadri-vitesse, obtenant ainsi le quadrivecteur énergie-impulsion :
Si on calcule la pseudo norme, on obtient :

La pseudonorme étant un invariant, on va pouvoir l'égaler à elle-même en la calculant dans différents référentiels avant et après un choc évènement par exemple.
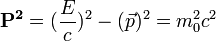
![\mathbf{P}=\begin{pmatrix}
\\ \frac {E}{c}\\
\ p_x\\
\ p_y\\
\ p_z\\\end{pmatrix} = \begin{bmatrix}
\gamma & \gamma\beta& 0 & 0\\
\gamma\beta & \gamma & 0& 0\\
0 & 0 & 1& 0\\
0 & 0 & 0& 1\end{bmatrix}\begin{pmatrix}
\\ \frac {E'}{c}\\
\ p'_x\\
\ p'_y\\
\ p'_z\\\end{pmatrix}= \mathbf{[\mathcal{L}]}*\mathbf{P'}](https://upload.wikimedia.org/math/d/a/4/da41eb5983c9ee1cf330c2a3f0b91b2a.png)
Dans la définition du quadrivecteur, on a posé : où E est l'énergie associée à la particule en mouvement. E = γ(V)m0c2
où E est l'énergie associée à la particule en mouvement. E = γ(V)m0c2
-
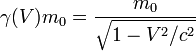 , quantité qui tend vers l'infini quand V tend vers c a souvent été utilisée au XXième siècle en terme de masse variable.
, quantité qui tend vers l'infini quand V tend vers c a souvent été utilisée au XXième siècle en terme de masse variable.
On préfère aujourd'hui réserver le mot masse pour désigner l'énergie propre d'une particule ; c’est-à-dire son énergie au repos.
Les chocs aux hautes énergies [modifier]
La principale confirmation de la relativité est aujourd'hui facilement illustrée par ce qu'on appelle la physique des particules ou encore des hautes énergies. Les accélérateurs de particules frappent par la dimension des installations ; ce sont des tubes (dans lequel on fait le vide) de plusieurs kilomètres en forme d'anneau creux ou tore dans lequel sont injectés des 'paquets' de protons qui circulent à grandes vitesses après avoir été accélérés par des champs électriques et déviés par des champs magnétiques qui leur imposent de rester à tourner dans le tube. Ainsi il est possible de faire des chocs de protons contre des protons à hautes énergies.
Référentiels particuliers [modifier]
On considère en général deux référentiels : le référentiel où la cible 2 est au repos dit du laboratoire SL
et le référentiel où le tout est immobile dit à tort du centre de masse SCM
Exemple de choc [modifier]
si on a une particule de masse m1 qui vient percuter une particule de masse m2, on écrira en relativité restreinte la conservation du quadrivecteur impulsion :
On suppose que les deux particules se sont provisoirement unies et forment le tout avec :

ce qui donne aussitôt dans le référentiel où 2 est immobile :

où Ec1 = E1 − m1c2 est l'énergie cinétique de la particule 1, puisque c'est son énergie en mouvement - moins son énergie au repos. en résolvant :

Remarquer que:
et

On peut donc en déduire le γ permettant de passer du système du laboratoire (cible 2 immobile) au système dit du centre de masse (l'ensemble est immobile)
et le :

On constate que la masse du tout mt n'est pas la somme des masses m1 et m2, alors que ce serait le cas classiquement. La conservation classique de la masse est mise à mal par la relativité restreinte et c'est là l'origine de l'énergie nucléaire : l'énergie du soleil provient de la libération de l'énergie contenue dans la masse qui disparaît dans les réactions de fusion. En sens inverse on peut créer de la masse et donc de nouvelles particules dans les anneaux de collission par la conversion d'énergie en masse.
- La pseudonorme du tout donne la masse totale exprimée dans SL en fonction de m1,m2 et Ec1.
Le défaut de masse [modifier]
Dans l'exemple précédent, mt était supérieure à la somme des masses m1 et m2. À l'inverse, lors d'une désintégration radioactive, la masse des particules formées est inférieure à la masse initiale. La réaction a produit de l'énergie : elle est exoénergétique. Ce qui donne aussitôt dans le référentiel dit du centre de masse celui où la particule mt est immobile :

où Ec2 = E2 − m2c2 est l'énergie cinétique de la particule 2, puisque c'est son énergie en mouvement - moins son énergie au repos. en ordonnant et en résolvant :

On peut donc en déduire le γ permettant de passer du système du laboratoire (cible 2 immobile) au système dit du centre de masse (l'ensemble est immobile)
et

et en permuttant 1 et 2
et le :


où Ec1 = E1 − m1c2 est l'énergie cinétique de la particule 2, puisque c'est son énergie en mouvement - moins son énergie au repos.

Remarquer que:
et
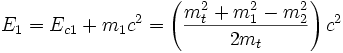
Les lois de l'électromagnétisme [modifier]
L'équation de conservation de la charge électrique s'écrit :
 La force de Lorentz s'écrit :
La force de Lorentz s'écrit :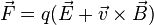
Les équations de Maxwell s'écrivent sous forme vectorielle
Écrites dans le formalisme de Lorentz avec des quadrivecteurs, elles se simplifient.
On pose comme quadri-vecteur courant  . En effet, soit ρ0 la densité de charge dans le référentiel propre, se déplaçant à la vitesse
. En effet, soit ρ0 la densité de charge dans le référentiel propre, se déplaçant à la vitesse 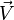 par rapport à un référentiel
par rapport à un référentiel  . Du fait de la contraction des longueurs dans la direction de
. Du fait de la contraction des longueurs dans la direction de 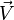 , le volume occupé par une charge donnée sera multiplié par le facteur
, le volume occupé par une charge donnée sera multiplié par le facteur  lorsqu'il est observé depuis le référentiel
lorsqu'il est observé depuis le référentiel  , et donc la densité de charge dans ce même référentiel sera γ(V)ρ0. Par ailleurs, la densité de courant est
, et donc la densité de charge dans ce même référentiel sera γ(V)ρ0. Par ailleurs, la densité de courant est  , de sorte que :
, de sorte que :
-
 produit de ρ0 par le quadrivecteur vitesse.
produit de ρ0 par le quadrivecteur vitesse.
On peut alors appliquer les transformations de Lorentz pour déterminer comment sont transformées densité de charge et densité de courant d'un référentiel  à un référentiel
à un référentiel  .
.
Nous avons donc comme formule de transformation des courants et des densités de courant (pour un référentiel en translation uniforme) :
De la même façon, on a comme transformation pour les potentiels :
On définit le quadri-potentiel électromagnétique :
- Nous définissons le champs électromagnétique de la façon suivante :

Les transformations des composantes du champ électromagnétique s'écrivent :
- On peut alors définir :
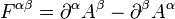
- Le Tenseur électromagnétique F est anti-symétrique, nous pouvons calculer ses composantes :

- Le tenseur électromagnétique s'écrit sous forme matricielle :
![F^{\alpha\beta}=\left[\begin{matrix}
0 & -\frac{E_x}{c} & -\frac{E_y}{c} & -\frac{E_z}{c}\\
\frac{E_x}{c} & 0 & -B_z & B_y\\
\frac{E_y}{c} & B_z & 0 & -B_x\\
\frac{E_z}{c} & -B_y & B_x & 0
\end{matrix}\right]](https://upload.wikimedia.org/math/0/0/4/00434fce2fb99b81ce2b089ed0b74a8c.png)
Les équations contenant les sources (1) et (4) s'écrivent dans la formulation covariante :
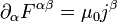
- En effet, on a :

- En effet, on a :
Les équations (2) et (3) s'écrivent :

- La vérification est aisée.
L'équation s'écrit aussi avec le tenseur de Lévi-Civita : 
Autres ébauches [modifier]
- les intervalles d'espace
- etc.