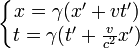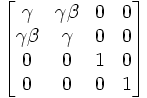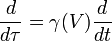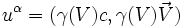PREUVE OVNI

Articles

Album photos

Forum

Discussions générales

Membres

502 membres

Pour être tenu au courant des futures mises à jour du blog et y participer, inscrivez-vous:

A découvrir

Statistiques

Total :
Aujourd'hui :
En ce moment :

Calculs relativistes - Partie 1

Calculs relativistes

Un article de Wikipédia, l'encyclopédie libre.

Aller à : Navigation, Rechercher

Cet article ne cite pas suffisamment ses sources.
Tous les articles de Wikipédia doivent être fondés sur des sources fiables et indépendantes. Améliorez la qualité ce cet article à l'aide des conseils sur les sources !

Cet article se veut volontairement calculatoire pour montrer que l'essentiel peut se déduire par le calcul des transformations de Lorentz.

Cet article de physique fait
partie de la série relativité

Avant Einstein

Histoire de la physique

Michelson - Lorentz

Mach - Poincaré - Hilbert

exp:Michelson et Morley - éther

Avec Einstein

Principe de relativité

c - transformation de Lorentz

espace-temps - E=mc² - temps

exp:pensée?-jumeaux-train

relativité restreinte-générale

Principe d'équivalence

controverse historique

En physique des particules

cyclotron

accélérateur de particules

Feynman - EQR

Méta

Formulaire de physique

Sommaire

[masquer]

Les transformations de Lorentz [modifier]

Soient deux référentiels $\mathbb{R}$ et $\mathbb R'$ en translation rectiligne l'un par rapport à l'autre sur des axes parallèles, avec une vitesse relative v selon l'axe Ox. Lorsque l'on passe du premier référentiel au second, les coordonnées sont liées par la transformation de Lorentz :

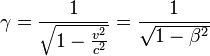$x' = \gamma (x - vt) \qquad y' = y \qquad z' = z \qquad t' = \gamma (t - \frac{vx}{c^2})$ avec $\gamma = \frac{1}{\sqrt{1- \frac{v^2}{c^2}}} = \frac{1}{\sqrt{1- \beta^2}}$ et $\beta = \frac{v}{c}$

Les transformations inverses 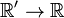$\mathbb R' \rightarrow \mathbb R$ qui donnent les coordonnées dans R en fonction des coordonnées dans R' s'en déduisent en résolvant le système de deux équations à deux inconnues $x' = \gamma (x - vt) \qquad t' = \gamma (t - \frac{vx}{c^2})$ Il suffit de changer le signe de la vitesse :

$x' = \gamma (x - vt) \qquad y' = y \qquad z' = z \qquad t' = \gamma (t - \frac{vx}{c^2})$
$\qquad x = \gamma (x' + vt') \qquad y = y' \qquad z = z' \qquad t = \gamma (t' + \frac{vx'}{c^2})$
On a donc en écriture matricielle :

$\begin{pmatrix} ct'\\x'\\y'\\z'\\\end{pmatrix} = \begin{bmatrix} \gamma & -\gamma\beta& 0 & 0\\ -\gamma\beta & \gamma & 0& 0\\ 0 & 0 & 1& 0\\ 0 & 0 & 0& 1\end{bmatrix}\begin{pmatrix} ct\\x\\y\\z\\\end{pmatrix}$
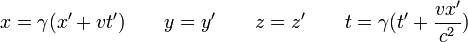
Et inversement : $\begin{pmatrix} ct\\x\\y\\z\\\end{pmatrix} = \begin{bmatrix} \gamma & +\gamma\beta& 0 & 0\\ +\gamma\beta & \gamma & 0& 0\\ 0 & 0 & 1& 0\\ 0 & 0 & 0& 1\end{bmatrix}\begin{pmatrix} ct'\\x'\\y'\\z'\\\end{pmatrix}$ Ceci est la façon matricielle d'écrire une transformation de Lorentz.

Vous pouvez constater que si vous remplacez x' et t' par leurs expressions données au dessus en fonction de x et t, vous obtenez x = x et t = t ce qui signifie que les formules ci-dessus sont inverses l'une de l'autre ; les mathématiciens expriment cela en disant que cette propriété est une des propriétés requises pour que les transformations de Lorentz forment un groupe, la principale conséquence étant que la composition de deux transformations de Lorentz est une transformation de Lorentz. On verra dans le paragraphe relatif à la composition des vitesses une utilisation du groupe de Lorentz.

Presque tout se déduit des transformations de Lorentz, ce qui fait dire que, en Relativité restreinte, il vaut mieux se fier aux résultats du calcul que de faire des raisonnements « fumeux » ! Noter que les transformations ci-dessus sont identiques aux transformations de Galilée pour les vitesses usuelles et cependant détruisent la notion du temps universel puisque celui-ci devient dépendant du référentiel : le temps varie comme la position varie. Le temps est une coordonnée pour exprimer les lois de la physique et celles-ci deviennent covariantes lorsque on les exprime avec un espace à 4 dimensions (ct, x, y, z). Note : en remplaçant ici t par ct, on ne fait que transformer les unités de temps de façon qu'elles soient en mètres plutôt qu'en secondes.

On va donc ci-dessous développer une page de calculs permettant de déduire des conséquences :

La pseudonorme [modifier]

On repère un évènement par les coordonnées d'un vecteur dans un repère à 4 dimensions c temps-espace $\mathbf{r}=( ct, \vec r) = (ct,x,y,z)$

On montre facilement que :

$\mathbf{r^2}=c^2t^2 - \vec r^2=c^2t^2 - (x^2+y^2+z^2)=c^2t'^2 - (x'^2+y'^2+z'^2)=c^2t'^2 - \vec{r'}^2=\mathbf{r'^2}$

En effet :

$\left(\gamma(ct'+\beta x')\right)^2 - (\left(\gamma(x'+\beta ct')\right)^2+y'^2+z'^2)=(\left(\gamma^2(1-\beta^2)\right) c^2t'^2 - ((\left(\gamma^2(1-\beta^2)\right)x'^2+y'^2+z'^2)=c^2t'^2 - (x'^2+y'^2+z'^2)$

On note en gras la pseudonorme du vecteur à 4 dimension ou quadrivecteur: $\mathbf{r^2}=c^2t^2 - \vec r^2$

ceci est appelé la pseudo - norme du quadrivecteur position d'un évènement repéré dans l'espace temps à 4 dimensions : On a montré mathématiquement que cette quantité ne dépend pas du référentiel et constitue donc un invariant aux transformations de Lorentz.

La dilatation des durées [modifier]

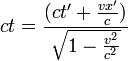
Déjà, il faut constater que au temps t' correspond une infinité de temps dans $\mathbb{R}$ : $ct = \frac{(ct'+\frac{vx'}{c})}{\sqrt{1 - {v^2 \over c^2}}}$

Pour simplifier , prenons t'=0: $ct = \frac{(\frac{vx'}{c})}{\sqrt{1 - {v^2 \over c^2}}}$

Pour le même temps t'=0 correspondent des temps t qui sont pour des x positifs dans le futur de $\mathbb{R}$ et pour des x négatifs dans le passé de $\mathbb{R}$ !

Soient deux référentiels, $\mathbb{R}$ , et $\mathbb{R'}$ en translation rectiligne uniforme par rapport au premier référentiel suivant l'axe des x positifs à la vitesse v.

Une horloge au repos dans $\mathbb{R'}$ au point $M'(x' o, y' o, z' o)$ , mesure deux évènements dans $\mathbb{R'}$ : $(c t' 1, x' o, y' o, z' o)$ et $(c t' 2, x' o, y' o, z' o)$ qui se produisent donc au même endroit et à des temps différents.

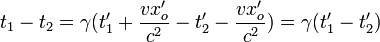
Noter que : $x 1 = γ(v t' 1 + x' o)$ et $x 2 = γ(v t' 2 + x' o)$ selon les transformations de changement de référentiel. La durée entre deux évènements dans le référentiel $\mathbb{R'}$ se produisant en $M'(x' o, y' o, z' o)$ est : $t' 1 - t' 2$ La durée entre ces deux évènements dans le référentiel $\mathbb{R}$ est : $t_1-t_2=\gamma(t'_1+\frac{vx'_o}{c^2}-t'_2-\frac{vx'_o}{c^2})=\gamma(t'_1-t'_2)$

En posant $τ 0 = t' 1 - t' 2$ la durée au repos, et $τ = t 1 - t 2$ la durée observée dans le référentiel $\mathbb{R}$ , nous obtenons la formule dite de dilatation des durées :

$\tau=\frac{\tau_0}{\sqrt{1-\frac{v^2}{c^2}}}$

Ainsi, vu du référentiel $\mathbb{R}$ par deux observateurs situés en $x 1 = γ(v t' 1 + x' o)$ et $x 2 = γ(v t' 2 + x' o)$ et qui ont synchronisé leurs horloges dans le référentiel $\mathbb{R}$ la mesure de l'intervalle de temps n'est pas égal à celui mesuré par un observateur immobile situé en $M'(x' o, y' o, z' o)$ :

La quantité $τ 0$ s'appelle temps propre . Comme 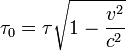$\tau_0 = \tau \sqrt{1 - {v^2 \over c^2}}$ , on voit que la quantité 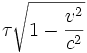$\tau \sqrt{1 - {v^2 \over c^2}}$ est un invariant relativiste ne dépendant pas du référentiel $\mathbb R$ choisi pour la mesurer.

Le facteur 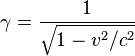$\gamma = {1 \over \sqrt{1 - v^2/c^2}}$ qui intervient dans la dilatation des durées, a, pour un avion, une valeur approchée de 1 + v²/2c² soit 1+10^(-10) =1.0000000001 Quelques microsecondes sur un an de vol de supersonique ! Difficile de croire à la réalisation d'une mesure de la dilatation du temps en comparant l'indication d'horloges demeurées au sol à l'indication d’horloges emportées sur un avion (cette expérience a eu lieu aux USA en 1972 de façon non probante). Néanmoins les chercheurs travaillant sur les particules produites dans les synchrotrons vivent quotidiennemnt l'effet de la dilatation du temps T= γ T'.

Et aujourd'hui,les horloges atomiques embarquées dans les satellites des systèmes GPS sont calibrées de façon à ce que leurs indications soient compatibles avec des horloges restées sur Terre.

Un satellite n'est pas en translation par rapport au référentiel de la Terre.

NON C'EST FAUX !!

La contraction des longueurs [modifier]

Nous nous plaçons dans les conditions évoquées au précédent paragraphe. Mesurer une longueur M₁M₂ revient à repérer dans un système de coordonnées les deux extrémités M₁ et M₂ ; Cela ne pose pas de problème si celles-ci ne bougent pas dans le temps ; par contre si elles se déplacent à la même vitesse v, il faudra repérer ces deux extrémités simultanément. Nous considérons donc une règle au repos dans $\mathbb{R'}$ , de longueur $L 0$ au repos. Les coordonnées de ses extrémités sont $x' 1$ et $x' 2$ . Les évènements de ses extrémités sont : $(t', x' 1,0,0)$ et $(t', x' 2,0,0)$ , car il faut observer simultanément ces évènements dans $\mathbb{R'}$ .

Considérons maintenant les évènements $(t' 1, x' 1,0,0)$ et $(t' 2, x' 2,0,0)$ , on obtient dans $\mathbb{R}$ :

$\begin{matrix}\left\{\begin{matrix} x_1=\gamma(x'_1+vt'_1)\\ t_1=\gamma(t'_1+\frac{v}{c^2}x'_1) \end{matrix}\right. &\left\{\begin{matrix} x_2=\gamma(x'_2+vt'_2)\\ t_2=\gamma(t'_2+\frac{v}{c^2}x'_2) \end{matrix}\right.\end{matrix}$

Déterminons $t' 2 - t' 1$ pour que ces évènements soient simultanés dans $\mathbb{R}$ , il faut que :

$t_2-t_1=\gamma(t'_2-t'_1+\frac{v}{c^2}(x'_2-x'_1))=0$ soit :

$t'_2-t'_1=-\frac{v}{c^2}(x'_2-x'_1)$

$x_2-x_1=\gamma(x'_2-x'_1)+\gamma v(t'_2-t'_1)=\frac{1}{\gamma}(x'_2-x'_1)$

La longueur de la règle, observée dans le référentiel $\mathbb{R}$ s'exprime :

$L=L_{0}\sqrt{1-\frac{v^2}{c^2}}$

Ainsi, la règle est plus courte dans le référentiel $\mathbb{R}$ que dans le référentiel $\mathbb{R}'$ : la règle M₁M₂ en mouvement est plus courte lorsque la mesure de sa longueur est faite dans un référentiel dans lequel M₁M₂ est en mouvement.

Ainsi un coureur R' de 100m va s'autochronométrer avec sa montre un temps propre de T'₀=10s sur une piste de L₀ = 100m dans R : pour le coureur, la piste qui défile à la vitesse v sous ses enjambées ne fait pas 100 m elle est contractée L'=L₀/γ ; par contre pour le juge de piste la piste est immobile par rapport à lui ; elle fait L₀ = 100m en longueur propre et le temps est T=γT'₀ c'est-à-dire dilaté. Le coureur et le juge ne sont d'accord ni sur le temps ni sur la distance, mais sont d'accord sur la vitesse v = L'/T'₀= L₀/T. Bien sûr, aux vitesses d'un coureur de 100m, toutes ces différences sont imperceptibles. Les effets relativistes ne sont perceptibles que à l'échelle nucléaire ou à l'échelle galactique.

La composition des vitesses [modifier]

Nous savons dans la vie quotidienne que les vitesses s'ajoutent. Prenons un exemple concret, je prends le métro, et je marche à 5 km/h sur un tapis roulant allant dans le même sens à 4 km/h. Ma vitesse par rapport au sol est de 9 km/h. Nous allons voir comment obtenir la formule de composition des vitesses galiléenne, puis relativiste. Nous supposerons dans ce paragraphe que tous les déplacements se font parallèlement à un même axe.

Cas galiléen [modifier]

Les transformations de Galilée sont :

$\left\{ \begin{matrix} x=x'+vt'\\ t=t' \end{matrix} \right.$

en différenciant, on obtient :

$\begin{matrix} dx=dx'+vdt'=(\frac{dx'}{dt'}+v)dt'\\ dt=dt' \end{matrix}$

le quotient donne : $u = u' + v$ , avec $u = {dx \over dt}$ et $u' = {dx' \over dt'}$ , ce qui est la loi de composition classique.

Cas relativiste [modifier]

Les transformations de Lorentz sont :

$\left\{ \begin{matrix} x=\gamma(x'+vt')\\ t=\gamma(t'+\frac{v}{c^2}x') \end{matrix} \right.$

en différenciant, on obtient :

$\begin{matrix} dx=\gamma(dx'+vdt')=\gamma(\frac{dx'}{dt'}+v)dt'\\ dt=\gamma(dt'+\frac{v}{c^2}dx')=\gamma(1+\frac{v}{c^2}\frac{dx'}{dt'})dt' \end{matrix}$

le quotient donne :

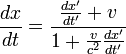$\frac{dx}{dt}=\frac{\frac{dx'}{dt'}+v}{1+\frac{v}{c^2}\frac{dx'}{dt'}}$ Soit : $u=\frac{u'+v}{1+\frac{u'v}{c^2}}$ la loi de composition relativiste des vitesses : elles ne s'ajoutent pas

On notera que, si u' = c, alors on obtient u = c. La vitesse de la lumière est la même dans les deux référentiels.

Utilisation du groupe de Lorentz [modifier]

Soit L(v) la matrice

$\begin{bmatrix} \gamma & \gamma\beta& 0 & 0\\ \gamma\beta & \gamma & 0& 0\\ 0 & 0 & 1& 0\\ 0 & 0 & 0& 1\end{bmatrix}$

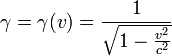avec $\beta = \beta(v) = {v \over c}$ et $\gamma = \gamma(v) = {1 \over \sqrt{1 - \frac{v^2}{c^2}}}$ . Cette matrice, appliquée aux composantes ${\mathbf{X'}}$ dans un référentiel $\mathbb R'$ donne les composantes ${\mathbf{X}}$ dans le référentiel $\mathbb R$ par rapport auquel $\mathbb R'$ se déplace avec une vitesse v :

$\mathbf{X} = L(v)\mathbf{X'}$

Si on dispose d'un référentiel $\mathbb R''$ se déplaçant par rapport au référentiel $\mathbb R'$ à la vitesse u', alors les relations entre les composantes $\mathbf{X''}$ dans le référentiel $\mathbb R''$ et les composantes $\mathbf{X'}$ dans le référentiel $\mathbb R'$ sont données par :

$\mathbf{X'} = L(u')\mathbf{X''}$

On a donc :

$\mathbf{X} = L(v)\mathbf{X'} = L(v)L(u')\mathbf{X''}$

La matrice produit $L (v) L (u')$ n'est autre que la matrice $L (u)$ , où u est la vitesse du référentiel $\mathbb R''$ par rapport au référentiel $\mathbb R$ . On vérifiera que $L(v)L(u') = L({u'+v \over 1+u'v/c^2})$ , et donc que $u=\frac{u'+v}{1+\frac{u'v}{c^2}}$ , comme plus haut.

On se reportera au paragraphe ci-dessous pour le cas plus général où les vitesses u et v ne sont pas colinéaires.

Le quadrivecteur vitesse [modifier]

Transformation des vitesses [modifier]

On peut calculer une vitesse en formant le rapport d'une distance par un temps :

$\frac{V_x}{c}= \frac{x}{ct} = \frac{\frac{x'}{ct'} + \beta}{1 +\beta\frac{x'}{ct'}} \qquad \frac{V_y}{c}= \frac{y}{ct} = \frac{\frac{y'}{ct'}}{\gamma (1 +\beta\frac{x'}{ct'})} \qquad \frac{V_z}{c}= \frac{z}{ct} = \frac{\frac{z'}{ct'}}{\gamma (1 +\beta\frac{x'}{ct'})} \qquad$

$\frac{V_x}{c}= \frac{\frac{V_x'}{c} + \beta}{1 + \beta{\frac{V_x'}{c}} } \qquad \frac{V_y}{c}= \frac{\frac{V'_y}{c} }{\gamma (1 + \beta{\frac{V_x'}{c}})} \qquad \frac{V_z}{c}= \frac{\frac{V'_z}{c} }{\gamma (1 + \beta{\frac{V_x'}{c}})} \qquad$

Ce sont les transformations sur les vitesses et l'on constate que les vitesses ne s'ajoutent pas : il ne faut pas appeler ces relations en utilisant le mot 'addition' par contre

Ces relations peuvent s'écrire différemment si on calcule :

$1-\frac{V^2}{c^2}=1-\frac{V_x^2+V_y^2+V_z^2}{c^2}=1- \left(\frac{\frac{V_x'}{c} +\beta}{1 + \beta{\frac{V_x'}{c}} }\right)^2- (1-\frac{v^2}{c^2})\left(\left(\frac{\frac{V_y'}{c} }{1 + \beta{\frac{V_x'}{c}} }\right)^2 +\left(\frac{\frac{V_z'}{c} }{1 + \beta{\frac{V_x'}{c}} }\right)^2\right)$

soit: $(1-\frac{V^2}{c^2})(1 + \beta\frac{V_x'}{c})^2=(1-\frac{V'^2}{c^2})(1-\frac{v^2}{c^2})$

En posant $\Gamma (V) = \frac {1}{\sqrt{1-\frac{V^2}{c^2}}}= \frac {1}{\sqrt{1-(\frac{x}{ct} )^2-(\frac{y}{ct} )^2-(\frac{z}{ct} )^2}}=\Gamma_V$ et $\Gamma (V') = \frac {1}{\sqrt{1-\frac{V'^2}{c^2}}}= \frac {1}{\sqrt{1-(\frac{x'}{ct'} )^2-(\frac{y'}{ct'} )^2-(\frac{z'}{ct'} )^2}}=\Gamma_{V'}$ et $\gamma = \gamma_v = \frac {1}{\sqrt{1-\frac{v^2}{c^2}}}$ .

s'écrit $(\Gamma_Vc) = \gamma_v\left( (\Gamma_{V'}c) + \beta(\Gamma_{V'}V_x') \right)$ . qui est une des transformations de Lorentz si on considère le quadrivecteur

$(\Gamma_V c, \Gamma_V\vec V )= \frac {(c,\vec V)}{\sqrt{1-\frac{V^2}{c^2}}}$ est le quadrivecteur vitesse.
de même :

$\Gamma_V c = \gamma_v ( \Gamma_{V'} c + \beta \Gamma_{V'} V_x')\qquad \Gamma_V V_x = \gamma_v ( \Gamma_{V'} V_x' + \beta \Gamma_{V'}c)$
$\qquad \Gamma_V V_y = \Gamma_{V'} V_y' \qquad \Gamma_V V_z = \Gamma_{V'} V_z'$

$\begin{pmatrix} \gamma (V) c\\ \gamma (V) V_x\\ \gamma (V) V_y\\ \gamma (V) V_z\\\end{pmatrix} = \begin{bmatrix} \gamma & \gamma\beta& 0 & 0\\ \gamma\beta & \gamma & 0& 0\\ 0 & 0 & 1& 0\\ 0 & 0 & 0& 1\end{bmatrix}\begin{pmatrix} \gamma (V') c\\ \gamma (V') V_x'\\ \gamma (V') V_y'\\ \gamma (V') V_z'\\\end{pmatrix}$
Ceci est la façon matricielle d'écrire une transformation de Lorentz sur les vitesses. où :

$(\gamma (V) c, \gamma (V)\vec V )= \frac {(c,\vec V)}{\sqrt{1-\frac{V^2}{c^2}}}$ est le quadrivecteur vitesse.
Ceci va avoir d'énormes conséquences en dynamique.

Utilisation des invariants:Pseudo-norme et Temps propre [modifier]

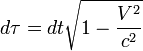considérons:: $ds=\sqrt{c^2dt^2-dx^2-dy^2-dz^2}$ et $d\tau=dt\sqrt{1-\frac{V^2}{c^2}}$ tous deux invariants.

c d τ = d s

En relativité restreinte, nous avons un invariant qui a pour dimension une longueur (que nous appelons longueur propre) : Nous définissons le temps propre de la manière suivante Nous obtenons :

$\frac{d}{d\tau}=\gamma(V)\frac{d}{dt}$

$d τ$ est l'accroissement de temps mesuré dans un référentiel en mouvement avec une vitesse V par rapport à un référentiel $\mathbb R$ dans lequel l'accroissement de temps est dt. La quantité $dt\sqrt{1-\frac{V^2}{c^2}}$ ne dépend pas du référentiel $\mathbb R$ choisi. C'est un invariant relativiste.

Nous définissons alors naturellement la quadrivitesse : $u^\alpha=\frac{dx^\alpha}{d\tau}$

$u^\alpha=({\gamma(V)}c,\gamma(V)\vec{V})$

qui a une pseudo norme égale à 1

Le voyage dans le futur des autres [modifier]

Ou le paradoxe des jumeaux :

Rappelons ce paradoxe :

On considère deux jumeaux A et B. A entreprend un long voyage puis revient vers B. A est alors censé avoir vieilli moins que B. Un paradoxe est soulevé si, en se plaçant du point de vue de A, il considère que c'est B qui voyage et qui devrait avoir moins vieilli que lui. Par conséquent, il n'y a aucune raison de trouver une dilatation du temps de l'un par rapport à l'autre.

Pour lever le paradoxe, il faut repérer où se situe une dissymétrie :

B se situe dans un référentiel inertiel $\mathbb R$ et n'en change pas. Dans un premier temps, A se situe dans un référentiel inertiel $\mathbb R'$ se déplaçant à la vitesse v par rapport à $\mathbb R$ , puis A fait demi-tour. Il change alors de référentiel inertiel et se trouve cette fois dans un référentiel inertiel $\mathbb R''$ se déplaçant à la vitesse -v par rapport à $\mathbb R$ .

La dissymétrie provient donc du fait que A change de référentiel inertiel, et pas B. Dans ce qui suit, on va illustrer par l'effet Doppler l'évolution des vies de A et de B. Nous verrons que lorsque A et B s'éloignent l'un de l'autre, l'effet Doppler des signaux qu'ils s'envoient l'un vers l'autre est identique (la fréquence des signaux est diminuée dans le même rapport). Lorsque A et B se rapprochent l'un de l'autre, il en est de même (la fréquence des signaux est augmentée dans le même rapport). Mais l'inversion de l'effet Doppler dépend uniquement de A, et B n'y joue aucun rôle. Ceci expliquera que, du point de vue de A ou de B, B a davantage vieilli que A.

On considère R' le référentiel du voyageur A qui se déplace à 3/5 c ce qui donne une dilatation du temps de

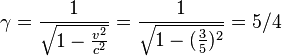
$\gamma = \frac {1}{\sqrt{1-\frac{v^2}{c^2}}}=\frac {1}{\sqrt{1-(\frac{3}{5})^2}}=5/4$

Si T₀ est la durée du voyage dans R', dans R le voyage aller a duré T₁ = γT₀ = 5/4 années, en parcourant vγT₀= 3/5×5/4 T₀ année-lumière= 3/4 T₀ a.l.

(a.l. signifie année-lumière ou distance parcourue par la lumière en un an)

Pour simplifier prenons un voyage de T₀ = 1 an et pour moderniser le voyage, O et O' sont sous vidéo avec émission en continu.

Par effet Doppler, les émissions sont reçues au ralenti avec un facteur (1+v/c) = 8/5 qui combiné avec la dilatation du temps 5/4 donne

$T_r = \frac {(1+v/c)}{\sqrt{1-\frac{v^2}{c^2}}} \times T_0= \sqrt{\frac {1+\frac{v}{c}}{1-\frac{v}{c}}} \times T_0=\frac {8}{5}\times \frac{5}{4}\times T_0= 2\times T_0$

Il faut donc à chacun, et la situation est symétrique pour B en O et A en O', le double de temps pour visionner en « direct » la vie de l'autre tant que ni l'un ni l'autre ne modifie son mouvement.

Supposons que A s'arrète au bout d'un an, sans revenir.

Point de vue de A : Il a reçu 6 mois de la vie de B au ralenti en un an de son trajet et recevra la suite de vie de B avec un retard de 3/4 d'an à un rythme normal. La dernière minute des six mois de la vie de B, visionnée au ralenti par A, a été émise 3/4 d'an plus tôt : A sait donc que B a vécu 5/4 d'année depuis son départ, ce qui est bien la durée T₁ du voyage de A dans le référentiel de B.

Point de vue de B : Après avoir reçu au ralenti le voyage aller de A en 2 ans, B reçoit la vie de A avec un retard de 3/4 d'an à un rythme normal. La dernière minute du voyage de A, visionnée au ralenti par B, a été émise 3/4 d'an plus tôt : B sait donc que le voyage de A a duré (dans le référentiel de B) 2 ans moins 3/4 année, soit 5/4 d'année, ce qui est bien la durée T₁ du voyage de A dans le référentiel de B.

Supposons maintenant que A en O' fasse demi tour au bout d'un an temps propre pour lui :

Point de vue de A : Il n'a alors visionné que 6 mois de la vie de B situé en O et il lui reste à recevoir ce qui est sur les 3/4 a.l qui séparent O de O', soit 3/4 ans du vécu de B en O non visionné par A situé en O', auquel il faudra ajouter la durée de vie de B pendant le voyage retour de A, soit T₁ = 5/4 ans de la vie de B. A recevra donc en accéléré, en un an de son voyage retour, 2 ans de vie de B en O, ce qui est bien conforme à une réception en accéléré due au fait que le voyage retour rapproche A et O. En effet :

$T_r = \frac {(1-v/c)}{\sqrt{1-\frac{v^2}{c^2}}} \times T_0= \sqrt{\frac {1-\frac{v}{c}}{1+\frac{v}{c}}} \times T_0=\frac {2}{5}\times \frac{5}{4}\times T_0= 1/2\times T_0$

A a donc voyagé pendant 2 ans et se retrouve avec B en O qui a vécu 6 mois + 2 ans = 2 ans et demi = 2T₁.

C'est l'effet dilatation du temps.

Noter que A a fait demi tour dans un espace contenant des ondes qui se propagent vers B en O.

Point de vue de B : En O, il reçoit pendant 2 ans le voyage aller de A en O' et lorsque A fait demi-tour, il ne le sait pas encore. Lorsqu'il reçoit l'information que A en O' a fait demi tour il y a déjà 3/4 d'an que A voyage sur le retour et A sera dans 6 mois en O : B en O reçoit ce retour d'un an de la vie de A en accéléré en ces 6 mois. B aura mis 2 ans et 6 mois pour recevoir les « 2ans » de voyage de A.

Tous les premiers de chaque mois, A et B s'envoient mutuellement le rang du mois qui commence pour eux. Dans le tableau ci-dessous, on affiche dans la colonne de gauche le rang vécu par A et qu'il envoie à B, alors que la colonne de droite affiche les messages que perçoit A de la part de B. Pendant le voyage aller, la vie de B s'affiche deux fois moins vite, alors que pendant le voyage retour, la vie de B s'affiche deux fois plus vite.

Point de vue de A
Horloge de A	Visionnage de la vie de B
A s'éloigne de B et visionne la vie de B au ralenti (deux fois moins vite)
1	1
2	1
3	2
4	2
...	...
10	5
11	6
12	6
A fait demi-tour. Il se rapproche de B et visionne la vie de B en accéléré (deux fois plus vite)
13	8
14	10
15	12
...	...
23	28
24	30

On peut procéder de même pour B. On prendra garde que A fait demi-tour au bout de 15 mois de B, mais que B ne le voit que 9 mois plus tard, le temps que le signal parvienne jusqu'à lui, donc au bout de 24 mois.

Point de vue de B
Horloge de B	Visionnage de la vie de A
A s'éloigne de B. B visionne sa vie au ralenti (deux fois moins vite)
1	1
2	1
3	2
4	2
...	...
22	11
23	12
24	12
B voit que A fait demi-tour. Il se rapproche de B et B visionne sa vie en accéléré (deux fois plus vite)
25	14
26	16
27	18
28	20
29	22
30	24

Le temps est relatif : comme une cordonnée, il dépend du référentiel. La durée du voyage de A, égal à 2T₀ est multiplié pour B par le facteur

$\frac {(1-v/c)}{\sqrt{1-\frac{v^2}{c^2}}}+ \frac {(1+v/c)}{\sqrt{1-\frac{v^2}{c^2}}}= \sqrt{\frac {1-\frac{v}{c}}{1+\frac{v}{c}}}+\sqrt{\frac {1+\frac{v}{c}}{1-\frac{v}{c}}}= \frac {2}{\sqrt{1-\frac{v^2}{c^2}}}$

Pour bien percevoir l'effet relativiste, il faut voir ce que donnerait le formalisme classique. Il suffit de supposer qu'au lieu de s'envoyer des messages électro-magnétiques, A et B s'envoie des messages sonores à intervalle régulier. Nous supposerons que le milieu dans lequel se déplacent ces ondes sonores coïncide avec le référentiel de B. Le facteur de l' effet Doppler demeure, mais au sens classique.

En ce qui concerne les messages émis de B vers A, A les perçoit à l'aller en ralenti avec le facteur $(1 - v / c)$ , et au retour en accéléré avec le facteur $(1 + v / c)$ , sans le facteur spécifiquement relativiste de dilatation du temps $\frac {1}{\sqrt{1-\frac{v^2}{c^2}}}$ . La longueur du trajet de A est 3cT₀/5, soit 3/5 a.l. (nous gardons les mêmes unités même si elles ne sont plus vraisemblables pour faciliter la comparaison).

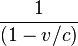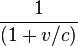En ce qui concerne les messages émis de A vers B, B les perçoit à l'aller de A en ralenti avec le facteur ${1 \over (1-v/c)}$ , et au retour de A en accéléré avec le facteur ${1 \over (1+v/c)}$ .

Point de vue de A : Pendant le voyage aller d'un an (sic), A reçoit au ralenti la vie de B avec un facteur 1 - 3/5, soit 2/5 de la vie de B. Au retour, A reçoit en accéléré la vie de B avec un facteur 1 + 3/5, soit 8/5 de la vie de B. Au cours de ses deux ans de voyage, A a visionné 2/5 + 8/5 = 2 années de la vie de B.

Point de vue de B : B reçoit au ralenti une année de voyage de A, avec un facteur 1/(1 + 3/5)) = 5/8. À cet instant, A fait demi-tour, mais B ne le sait pas encore. Il le saura lorsque le signal émis par A lui parviendra, c’est-à-dire dans 3/5 d'année. B verra donc s'écouler 1 + 3/5 = 8/5 d'années pour visionner la totalité du voyage de A avant de le voir faire demi-tour. Ces 8/5 d'années correspondent bien à un an de la vie de A visionnée au ralenti avec un facteur 5/8. Lorsque B voit A faire demi-tour, A est déjà sur le chemin du retour depuis 3/5 d'année. Il lui reste donc 2/5 d'année à voyager. B, quant à lui, visionnera en accéléré la totalité du voyage retour avec un facteur 1/(1 - 3/5)) = 5/2. Ce visionnage du retour durera donc également 2/5 d'année, et B aura visionné 8/5 + 2/5 = 2 années de voyage de A.

L'aller et le retour de A ont duré chacun 1 an, A a vécu 2 ans. Et B a vécu 2 ans pour visionner les 2 ans du voyage de A : classique quoi ! Le temps est le même pour A et B : universel.

16/09/2007

0 J'aime 0 Poster un commentaire

A découvrir aussi

Retour aux articles de la catégorie * UNIVERS, COSMOLOGIE -

⨯

Inscrivez-vous au blog

Soyez prévenu par email des prochaines mises à jour

Rejoignez les 502 autres membres